Primjer 2 (MNM Predavanje, zadatak 8.) Nađite sve cijele brojeve  i
i  koji zadovoljavaju jednadžbu:
koji zadovoljavaju jednadžbu: 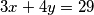
Rješenje:
 Budući da je
Budući da je  cijeli broj,
cijeli broj, 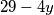 mora biti djeljivo s
mora biti djeljivo s  , odnosno
, odnosno 
Otkrili smo da 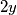 daje ostatak
daje ostatak  pri dijeljenju s
pri dijeljenju s  .
.  može biti broj oblika
može biti broj oblika 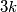 ,
, 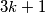 ili
ili 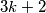 za neki cijeli broj
za neki cijeli broj  . Ako je
. Ako je 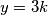 , onda je
, onda je 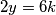 djeljiv s
djeljiv s  , što ne vrijedi. Ako je
, što ne vrijedi. Ako je 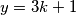 , onda
, onda 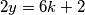 daje ostatak
daje ostatak  pri dijeljenju s
pri dijeljenju s  , što isto ne vrijedi. Ako je
, što isto ne vrijedi. Ako je 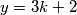 , onda
, onda 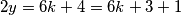 daje ostatak
daje ostatak  pri dijeljenju s
pri dijeljenju s  , što vrijedi!
, što vrijedi!
Dakle, dobili smo 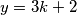 za
za 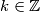 . Sada imamo
. Sada imamo 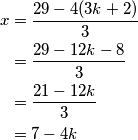
Našli smo sve cijele brojeve koji zadovoljavaju jednadžbu 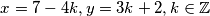
Za provjeru, možemo uvrstiti  i
i  u početnu jednadžbu i dobijamo
u početnu jednadžbu i dobijamo 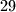 .
.
Za nastavak, upišite ime starogrčkog matematičara po kojem ime nose jednadžbe čija su rješenja cijeli brojevi, kakvu smo upravo i rješavali.
\textbf{Primjer 2} (\textit{MNM Predavanje, zadatak 8.})
Nađite sve cijele brojeve $x$ i $y$ koji zadovoljavaju jednadžbu:
\[
3x+4y=29
\]
\textbf{Rješenje:}
\begin{align*}
3x+4y&=29 \tag{izrazimo $x$}\\
x&= \frac{29-4y}{3}
\end{align*}
Budući da je $x$ cijeli broj, $29-4y$ mora biti djeljivo s $3$, odnosno
\begin{align*}
29-4y &\equiv 0 \mod{3} \\
-4y &\equiv -29 \mod{3} \\
4y &\equiv 29 \equiv 2 \mod{3} \tag{Zašto smijemo dijeliti s 2?}\\
2y &\equiv 1 \mod{3}
\end{align*}
Otkrili smo da $2y$ daje ostatak $1$ pri dijeljenju s $3$. $y$ može biti broj oblika $3k$, $3k+1$ ili $3k+2$ za neki cijeli broj $k$. Ako je $y=3k$, onda je $2y=6k$ djeljiv s $3$, što ne vrijedi. Ako je $y=3k+1$, onda $2y=6k+2$ daje ostatak $2$ pri dijeljenju s $3$, što isto ne vrijedi. Ako je $y=3k+2$, onda $2y=6k+4=6k+3+1$ daje ostatak $1$ pri dijeljenju s $3$, što vrijedi!
Dakle, dobili smo
\[
y=3k+2
\]
za $k\in \mathbb{Z}$. Sada imamo
\begin{align*}
x&= \frac{29-4(3k+2)}{3} \\
&= \frac{29-12k-8}{3} \\
&= \frac{21-12k}{3} \\
&= 7-4k
\end{align*}
Našli smo sve cijele brojeve koji zadovoljavaju jednadžbu
\[
x=7-4k, y=3k+2, k\in\mathbb{Z}
\]
Za provjeru, možemo uvrstiti $x$ i $y$ u početnu jednadžbu i dobijamo $29$.
Za nastavak, upišite ime starogrčkog matematičara po kojem ime nose jednadžbe čija su rješenja cijeli brojevi, kakvu smo upravo i rješavali.
 i
i  koji zadovoljavaju jednadžbu:
koji zadovoljavaju jednadžbu: 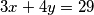
 Budući da je
Budući da je  cijeli broj,
cijeli broj, 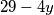 mora biti djeljivo s
mora biti djeljivo s  , odnosno
, odnosno 
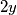 daje ostatak
daje ostatak  pri dijeljenju s
pri dijeljenju s  .
.  može biti broj oblika
može biti broj oblika 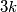 ,
, 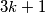 ili
ili 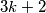 za neki cijeli broj
za neki cijeli broj  . Ako je
. Ako je 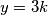 , onda je
, onda je 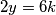 djeljiv s
djeljiv s  , što ne vrijedi. Ako je
, što ne vrijedi. Ako je 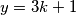 , onda
, onda 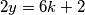 daje ostatak
daje ostatak  pri dijeljenju s
pri dijeljenju s  , što isto ne vrijedi. Ako je
, što isto ne vrijedi. Ako je 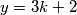 , onda
, onda 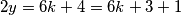 daje ostatak
daje ostatak  pri dijeljenju s
pri dijeljenju s  , što vrijedi!
, što vrijedi!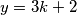 za
za 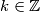 . Sada imamo
. Sada imamo 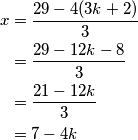
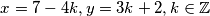
 i
i  u početnu jednadžbu i dobijamo
u početnu jednadžbu i dobijamo 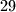 .
.