Potpuni kvadrati
Primjer 3: (Zayaan Mulla) Dokaži da niti jedan broj u nizu 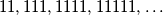 nije potpun kvadrat.
nije potpun kvadrat.
Rješenje:
Čest trik je gledati npr. ostatak potpunog kvadrata pri dijeljenju sa četiri. Ako je cijeli broj  paran,
paran, 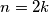 , onda njegov kvadrat daje ostatak
, onda njegov kvadrat daje ostatak  pri dijeljenju sa četiri.
pri dijeljenju sa četiri. 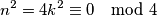 Ako je
Ako je  neparan,
neparan, 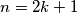 , onda njegov kvadrat daje ostatak
, onda njegov kvadrat daje ostatak  pri dijeljenju s četiri.
pri dijeljenju s četiri. 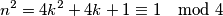 Dakle, kvadrat nekog broja može davati jedino ostatke
Dakle, kvadrat nekog broja može davati jedino ostatke  ili
ili  pri dijeljenju sa četiri.
pri dijeljenju sa četiri.
Prisjetimo se pravila djeljivosti: ako je broj koji formiraju zadnje dvije znamenke broja djeljiv sa četiri, onda je i taj broj djeljiv sa četiri. Kad bi brojevi u nizu završavali s  , onda bi davali ostatak
, onda bi davali ostatak  pri dijeljenju sa četiri
pri dijeljenju sa četiri  Budući da su brojevi u nizu za
Budući da su brojevi u nizu za  manji, oni daju ostatak
manji, oni daju ostatak  pri dijeljenju sa četiri.
pri dijeljenju sa četiri. 
No pokazali smo da potpuni kvadrati daju ostatak  ili
ili  pri dijeljenju s četiri. Zaključujemo da zato ni jedan broj u nizu nije potpun kvadrat.
pri dijeljenju s četiri. Zaključujemo da zato ni jedan broj u nizu nije potpun kvadrat.
Može li koji broj u nizu 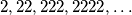 biti potpun kvadrat? Zašto?
biti potpun kvadrat? Zašto?
Upišite "Da" ili "Ne" kao odgovor.
