Primjer 1: Odredi sve parove prirodnih brojeva  za koje vrijedi
za koje vrijedi 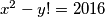
Rješenje: Broj 2016 je djeljiv brojem 32 i nije djeljiv brojem 64.
Uočimo da ne može vrijediti 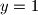 . Dakle, mora vrijediti
. Dakle, mora vrijediti 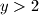 pa je
pa je 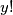 paran. Zato
paran. Zato  mora biti paran broj. Budući da su onda i
mora biti paran broj. Budući da su onda i  i 2016 djeljivi s 4, i
i 2016 djeljivi s 4, i 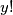 mora biti djeljivo s 4, pa je
mora biti djeljivo s 4, pa je  . Sada možemo zaključiti da je
. Sada možemo zaključiti da je 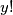 djeljivo sa 8, pa
djeljivo sa 8, pa  mora biti djeljivo s 8.
mora biti djeljivo s 8.
To znači da  mora biti djeljiv s 4, odnosno da je
mora biti djeljiv s 4, odnosno da je  djeljivo sa 16. Dakle,
djeljivo sa 16. Dakle, 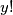 je djeljivo sa 16, pa je
je djeljivo sa 16, pa je 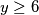 .
.
Ako je 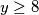 onda je
onda je 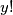 djeljivo sa 128, a posebno i s 32 pa
djeljivo sa 128, a posebno i s 32 pa  mora biti djeljivo s 32.
mora biti djeljivo s 32.
To znači da  nmora biti djeljiv barem sa 8, odnosno da je
nmora biti djeljiv barem sa 8, odnosno da je  djeljivo i sa 64.
djeljivo i sa 64.
Iz toga bi slijedilo da je 2016 djeljivo sa 64, što nije istina. Zato je 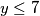 .
.
Provjerom vidimo da  nije potpun kvadrat, a
nije potpun kvadrat, a 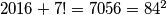 , pa je jedino rješenje
, pa je jedino rješenje 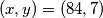 .
.
Za rješenje upišite  .
.
\textbf{Primjer 1:}
Odredi sve parove prirodnih brojeva $(x,y)$ za koje vrijedi $x^2-y!=2016$
\textbf{Rješenje:}
Broj 2016 je djeljiv brojem 32 i nije djeljiv brojem 64.\\\\
Uočimo da ne može vrijediti $y=1$. Dakle, mora vrijediti $y>2$ pa je $y!$ paran. Zato
$x$ mora biti paran broj.
Budući da su onda i $x^2$
i 2016 djeljivi s 4, i $y!$ mora biti djeljivo s 4, pa je $y\geq4$. Sada možemo zaključiti da je $y!$ djeljivo sa 8, pa $x^2$ mora biti djeljivo s 8.\\\\ To znači da
$x$ mora biti djeljiv s 4, odnosno da je $x^2$ djeljivo sa 16. Dakle, $y!$ je djeljivo sa 16, pa
je $y\geq6$.\\\\
Ako je $y\geq8$ onda je $y!$ djeljivo sa 128, a posebno i s 32 pa $x^2$ mora biti djeljivo s 32. \\\\
To znači da $x$nmora biti djeljiv barem sa 8, odnosno da je $x^2$ djeljivo i sa 64.\\\\
Iz toga bi slijedilo da je 2016 djeljivo sa 64, što nije istina. Zato je $y \leq 7$.\\
Provjerom vidimo da $2016 + 6!$ nije potpun kvadrat, a $2016 + 7! = 7056 = 84^2$, pa je
jedino rješenje $(x,y)=(84, 7)$.
Za rješenje upišite $1$.
 za koje vrijedi
za koje vrijedi 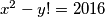
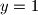 . Dakle, mora vrijediti
. Dakle, mora vrijediti 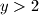 pa je
pa je 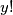 paran. Zato
paran. Zato  mora biti paran broj. Budući da su onda i
mora biti paran broj. Budući da su onda i  i 2016 djeljivi s 4, i
i 2016 djeljivi s 4, i 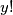 mora biti djeljivo s 4, pa je
mora biti djeljivo s 4, pa je  . Sada možemo zaključiti da je
. Sada možemo zaključiti da je 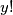 djeljivo sa 8, pa
djeljivo sa 8, pa  mora biti djeljivo s 8.
mora biti djeljivo s 8. mora biti djeljiv s 4, odnosno da je
mora biti djeljiv s 4, odnosno da je  djeljivo sa 16. Dakle,
djeljivo sa 16. Dakle, 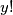 je djeljivo sa 16, pa je
je djeljivo sa 16, pa je 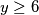 .
.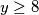 onda je
onda je 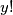 djeljivo sa 128, a posebno i s 32 pa
djeljivo sa 128, a posebno i s 32 pa  mora biti djeljivo s 32.
mora biti djeljivo s 32.  nmora biti djeljiv barem sa 8, odnosno da je
nmora biti djeljiv barem sa 8, odnosno da je  djeljivo i sa 64.
djeljivo i sa 64.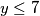 .
. nije potpun kvadrat, a
nije potpun kvadrat, a 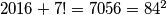 , pa je jedino rješenje
, pa je jedino rješenje 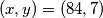 .
. .
. 