Vrijeme: 01:53
Djeljivost, prosti brojevi i kanonski zapis - Primjer 2
Primjer 1: Skup prostih brojeva je beskonačan.
Rješenje: Kako bi dokazali tvrdnju, često je korisno pretpostaviti suprotno i pokazati da u tom slučaju dolazimo do kontradikcije.
Pretpostavimo da su 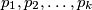 svi prosti brojevi. Promotrimo broj
svi prosti brojevi. Promotrimo broj 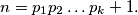 Uočimo da
Uočimo da  nije djeljiv s
nije djeljiv s 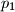 (jer
(jer 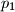 dijeli
dijeli 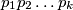 , a ne dijeli 1), isto tako pokažemo da nije djeljiv ni s
, a ne dijeli 1), isto tako pokažemo da nije djeljiv ni s 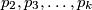 . Dakle, svaki prosti djelitelj od
. Dakle, svaki prosti djelitelj od  je različit od
je različit od 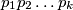 . Znamo da je
. Znamo da je  produkt prostih brojeva, pa postoji
produkt prostih brojeva, pa postoji  koji dijeli
koji dijeli  . Tako smo dobili novi prost broj pa je početna pretpostavka kriva i prostih brojeva ne postoji konačno, već beskonačno.
. Tako smo dobili novi prost broj pa je početna pretpostavka kriva i prostih brojeva ne postoji konačno, već beskonačno.
Za rješenje upišite  .
.
