MetaMath '22

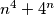\textbf{Primjer 1:} Odredite sve prirodne brojeve $n$ za koje je $n^4+4^n$ prost broj. \textbf{Rješenje:} Koristiti ćemo poznati identitet {\textit{Sophie Germain identity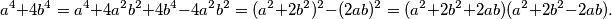}}: $$a^4 + 4b^4 = a^4 + 4a^2b^2 + 4b^4 - 4a^2b^2 = (a^2 + 2b^2)^2 - (2ab)^2= (a^2 + 2b^2 + 2ab)(a^2 + 2b^2 - 2ab).$$ Sada se vratimo na naš problem, ako je n paran broj, 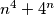$n^4+4^n$ je također paran i veći od 2 pa nije prost. Postavimo 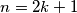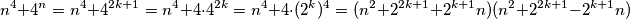$n = 2k+1$. $$n^4+4^n = n^4 + 4^{2k+1} = n^4 + 4\cdot4^{2k} = n^4 + 4\cdot (2^k)^4 = (n^2+2^{2k+1}+2^{k+1}n)(n^2+2^{2k+1}-2^{k+1}n)$$ Kako bi 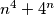$n^4+4^n$ bio prost broj moralo bi vrijediti 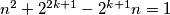$n^2+2^{2k+1}-2^{k+1}n = 1$. 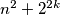Prema $A-G$ nejednakosti (na $n^2+2^{2k}$) dobivamo 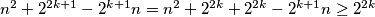$n^2+2^{2k+1}-2^{k+1}n = n^2+2^{2k} +2^{2k}-2^{k+1}n \geq 2^{2k}$ što je veće od 1 za 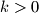$k>0$ pa je jedina opcija 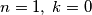$n=1, \; k=0$ i vidimo u tom slučaju $n^4+4^n = 5$ jest prost broj. Za rješenje upišite $1$.