U raznostraničnom trokutu $ABC$ simetrala kuta $\angle BAC$ siječe stranicu $\overline{BC}$ u točki $D$. Neka je $M$ točka stranici $\overline{AB}$ takva da je $|BM|=|BD|$, a $N$ točka na produžetku stranice $\overline{AC}$, preko vrha $C$, takva da je $|CN|=|CD|$. Dokaži da su kutovi $\angle DMA$ i $\angle NDA$ sukladni. \\\\
\textit{Rješenje.} \\\\
\includegraphics[scale=0.7]{Primjer1.PNG} \\\\
Trokut $DMB$ je jednakokračan pa je $\angle BMD=90^{\circ}-\dfrac{\angle ABC}{2}$. Kako je $\angle DMA$ vanjski kut trokuta $DMB$, vrijedi
$$
\angle DMA=180^\circ - \angle DMB=180^\circ-\left( 90^{\circ}-\dfrac{\angle ABC}{2}\right)=90^{\circ}+\dfrac{\angle ABC}{2}.
$$
Budući da je trokut $DNC$ jednakokračan, slijedi da je $\angle AND=\dfrac{\angle BCA}{2}$. \\\\
Promatrajmo sada trokut $NAD$. Za kut $\angle NDA$ vrijedi
\begin{align*}
\angle NDA &= 180^\circ - \angle DAN - \angle AND \\
&=180^{\circ}-\dfrac{\angle BAC}{2}-\dfrac{\angle BCA}{2} \\
&=180^{\circ}-\dfrac{\angle BAC+\angle BCA}{2} \\
&=180^{\circ}-\dfrac{180^\circ-\angle ABC}{2} \\
&=90^{\circ}+\dfrac{\angle ABC}{2}
\end{align*}
Dakle, $\angle DMA=\angle NDA=90^{\circ}+\dfrac{\angle ABC}{2}$.
Kao rješenje upišite zbroj veličina unutarnjih kutova trokuta.
 simetrala kuta
simetrala kuta  siječe stranicu
siječe stranicu  u točki
u točki  . Neka je
. Neka je  točka stranici
točka stranici  takva da je
takva da je 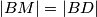 , a
, a  točka na produžetku stranice
točka na produžetku stranice  , preko vrha
, preko vrha  , takva da je
, takva da je 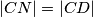 . Dokaži da su kutovi
. Dokaži da su kutovi 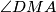 i
i  sukladni.
sukladni. 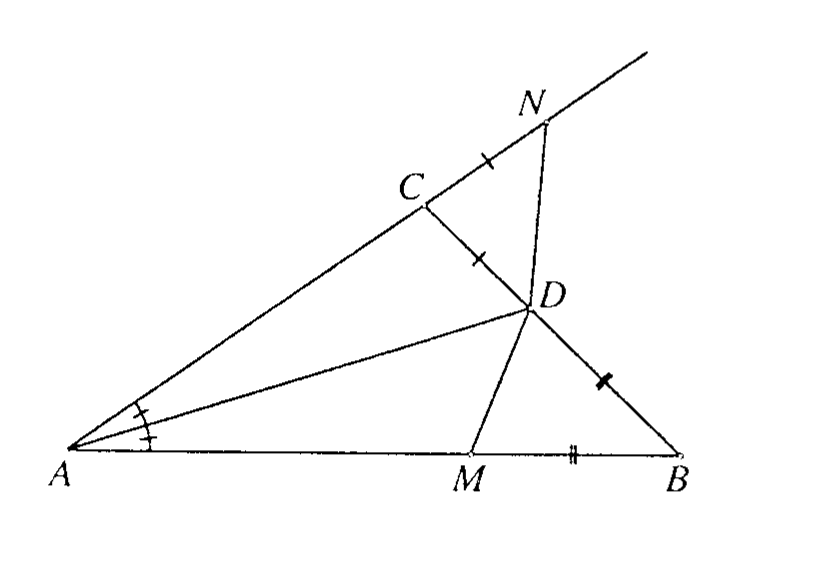
 je jednakokračan pa je
je jednakokračan pa je 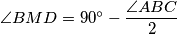 . Kako je
. Kako je 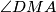 vanjski kut trokuta
vanjski kut trokuta  , vrijedi
, vrijedi 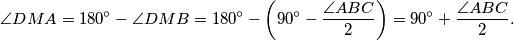 Budući da je trokut
Budući da je trokut 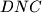 jednakokračan, slijedi da je
jednakokračan, slijedi da je  .
. 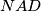 . Za kut
. Za kut  vrijedi
vrijedi 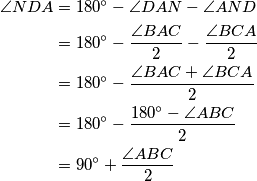 Dakle,
Dakle, 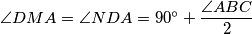 .
.