Vrijeme: 01:53
Angle Chasing - Primjer 2
Nad stranicama  i
i  šiljastokutnog trokuta
šiljastokutnog trokuta  s vanjske su strane nacrtani kvadrati
s vanjske su strane nacrtani kvadrati 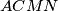 i
i 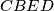 . Dokažite da je
. Dokažite da je 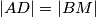 i
i 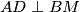 .
.
Rješenje. 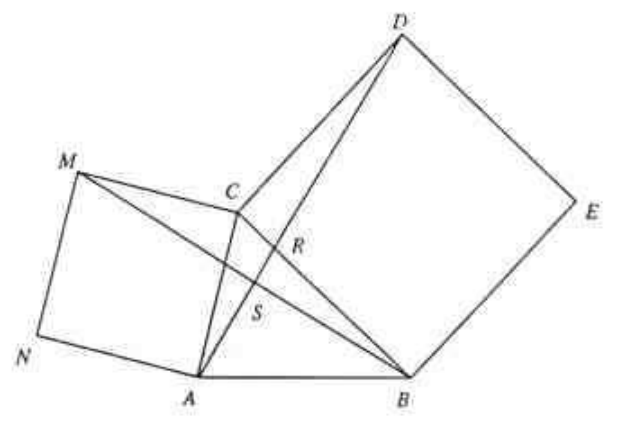
Vrijedi  i
i  . Osim toga,
. Osim toga, 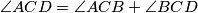 i
i 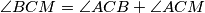 pa zbog
pa zbog 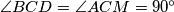 slijedi da je
slijedi da je 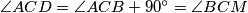 . Prema teoremu o sukladnosti trokuta SKS vrijedi
. Prema teoremu o sukladnosti trokuta SKS vrijedi 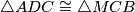 . Stoga je i
. Stoga je i 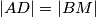 .
.
Neka je točka  presjek pravaca
presjek pravaca  i
i 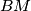 , a točka
, a točka  presjek pravaca
presjek pravaca  i stranice
i stranice  trokuta
trokuta  . Okomitost ćemo dokazati tako da promatramo kutove trokuta
. Okomitost ćemo dokazati tako da promatramo kutove trokuta 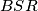 i
i  . Ako su to kutovi s okomitim pravca, tvrdnja je dokazana.
. Ako su to kutovi s okomitim pravca, tvrdnja je dokazana.
Zbog dokazane sukladnosti vrijedi 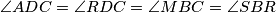 , a posebno promatramo
, a posebno promatramo 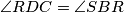 . Vrijedi i
. Vrijedi i 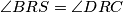 jer su to vršni kutovi. Zaključujemo da trokuti
jer su to vršni kutovi. Zaključujemo da trokuti 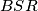 i
i  imaju dva para sukladnih kutova pa mora i treći par kutova biti sukladan. Zato je
imaju dva para sukladnih kutova pa mora i treći par kutova biti sukladan. Zato je  , iz čega slijedi
, iz čega slijedi 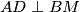 .
.
Kao rješenje upišite veličinu kuta kvadrata.
