Angle Chasing - Primjer 3
U trokutu  poznate su duljine dviju stranica,
poznate su duljine dviju stranica, 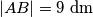 ,
, 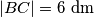 i veličina kuta između njih
i veličina kuta između njih 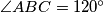 . Simetrala kuta
. Simetrala kuta  siječe stranicu
siječe stranicu  u točki
u točki  . Odredite
. Odredite 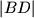 .
.
Rješenje. 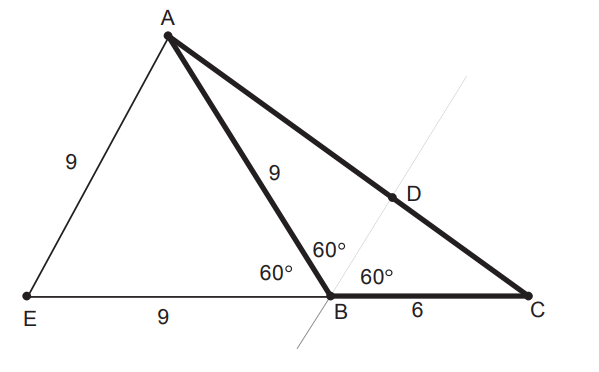
Simetrala kuta  dijeli kut na dva sukladna kuta veličine
dijeli kut na dva sukladna kuta veličine 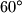 . Kada god imamo kutove te veličine, cilj je naći neki jednakostranični trokut.
. Kada god imamo kutove te veličine, cilj je naći neki jednakostranični trokut.
Produljimo stranicu  trokuta
trokuta  preko točke
preko točke  . Točkom
. Točkom  nacrtajmo pravac paralelan sa simetralom kuta
nacrtajmo pravac paralelan sa simetralom kuta  . Sjecište tog pravca i pravca
. Sjecište tog pravca i pravca  označimo sa
označimo sa  .
.
Kutovi 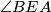 i
i 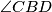 imaju paralelne krakove pa je
imaju paralelne krakove pa je 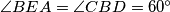 . Također
. Također 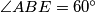 jer je to vanjski kut kuta
jer je to vanjski kut kuta 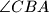 . Dakle, i treći kut u tom trokutu
. Dakle, i treći kut u tom trokutu 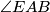 mora imati veličinu
mora imati veličinu 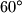 . Dakle, trokut
. Dakle, trokut 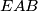 je jednakostraničan s duljinama stranica
je jednakostraničan s duljinama stranica 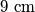 .
.
Trokut 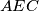 je sličan trokutu
je sličan trokutu 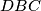 zbog KK teorema o sličnosti trokuta gdje je
zbog KK teorema o sličnosti trokuta gdje je 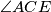 zajednički kut oba trokuta, a
zajednički kut oba trokuta, a 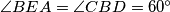 . Imamo:
. Imamo: 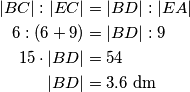
Kao rješenje upišite veličinu kuta jednakostraničnog trokuta.
