Neka su točke  i
i  sjecišta kružnica
sjecišta kružnica  i
i  . Neka su pravci
. Neka su pravci  i
i  kroz točku
kroz točku  takvi da
takvi da  siječe
siječe  i u točki
i u točki  , a
, a  i u točki
i u točki  i
i  siječe
siječe  i u točki
i u točki  , pri čemu točke
, pri čemu točke  ,
,  ,
,  ,
,  pripadaju istoj poluravnini u odnosu na pravac
pripadaju istoj poluravnini u odnosu na pravac  i točka
i točka  se nalazi unutar kuta
se nalazi unutar kuta  . Dokažite da je
. Dokažite da je 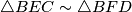 .
.
Rješenje.
Neka je 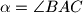 i
i 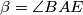 . S obzirom da su
. S obzirom da su  i
i 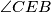 obodni kutovi u
obodni kutovi u  nad
nad  i jedan je šiljasti, a drugi tupi, onda je
i jedan je šiljasti, a drugi tupi, onda je 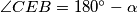 .
.
Kako su 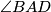 i
i 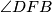 obodni kutovi u
obodni kutovi u  nad
nad  i jedan je šiljasti, a drugi tupi, onda je
i jedan je šiljasti, a drugi tupi, onda je 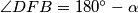 . Dakle,
. Dakle, 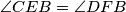 .
.
S obzirom da su 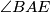 i
i 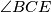 obodni kutovi u
obodni kutovi u  nad
nad 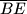 , onda je
, onda je 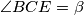 .
.
Kako su  i
i 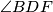 obodni kutovi u
obodni kutovi u  and
and 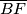 , onda je
, onda je 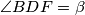 .
.
Dakle, 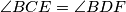 . Prema KK teoremu o sličnosti trokuta slijedi tvrdnja.
. Prema KK teoremu o sličnosti trokuta slijedi tvrdnja.
Kao rješenje upišite veličinu jednog kuta koji nastaje kada se konstruira simetrala pravog kuta.
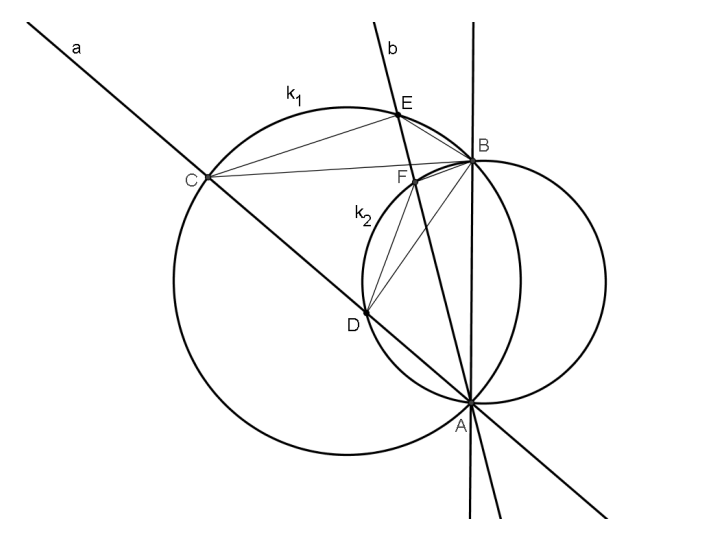
Neka su točke $A$ i $B$ sjecišta kružnica $k_1$ i $k_2$. Neka su pravci $a$ i $b$ kroz točku $A$ takvi da $a$ siječe $k_1$ i u točki $C$, a $k_2$ i u točki $D$ i $b$ siječe $k_1$ i u točki $F$, pri čemu točke $C$, $D$, $E$, $F$ pripadaju istoj poluravnini u odnosu na pravac $AB$ i točka $E$ se nalazi unutar kuta $\angle BAC$. Dokažite da je $\triangle BEC\sim \triangle BFD$. \\\\
\textit{Rješenje.} \\\\
\includegraphics[scale=0.6]{Primjer4.PNG} \\\\
Neka je $\alpha=\angle BAC$ i $\beta=\angle BAE$. S obzirom da su $\angle BAC$ i $\angle CEB$ obodni kutovi u $k_1$ nad $\overline{BC}$ i jedan je šiljasti, a drugi tupi, onda je $\angle CEB=180^\circ-\alpha$. \\\\
Kako su $\angle BAD$ i $\angle DFB$ obodni kutovi u $k_2$ nad $\overline{BD}$ i jedan je šiljasti, a drugi tupi, onda je $\angle DFB=180^\circ-\alpha$. Dakle, $\angle CEB=\angle DFB$. \\\\
S obzirom da su $\angle BAE$ i $\angle BCE$ obodni kutovi u $k_1$ nad $\overline{BE}$, onda je $\angle BCE=\beta$. \\\\
Kako su $\angle BAF$ i $\angle BDF$ obodni kutovi u $k_2$ and $\overline{BF}$, onda je $\angle BDF=\beta$.
\\\\
Dakle, $\angle BCE=\angle BDF$. Prema KK teoremu o sličnosti trokuta slijedi tvrdnja.
\\\\
Kao rješenje upišite veličinu jednog kuta koji nastaje kada se konstruira simetrala pravog kuta.
 i
i  sjecišta kružnica
sjecišta kružnica  i
i  . Neka su pravci
. Neka su pravci  i
i  kroz točku
kroz točku  takvi da
takvi da  siječe
siječe  i u točki
i u točki  , a
, a  i u točki
i u točki  i
i  siječe
siječe  i u točki
i u točki  , pri čemu točke
, pri čemu točke  ,
,  ,
,  ,
,  pripadaju istoj poluravnini u odnosu na pravac
pripadaju istoj poluravnini u odnosu na pravac  i točka
i točka  se nalazi unutar kuta
se nalazi unutar kuta  . Dokažite da je
. Dokažite da je 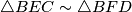 .
. 
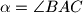 i
i 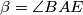 . S obzirom da su
. S obzirom da su  i
i 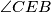 obodni kutovi u
obodni kutovi u  nad
nad  i jedan je šiljasti, a drugi tupi, onda je
i jedan je šiljasti, a drugi tupi, onda je 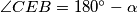 .
. 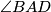 i
i 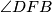 obodni kutovi u
obodni kutovi u  nad
nad  i jedan je šiljasti, a drugi tupi, onda je
i jedan je šiljasti, a drugi tupi, onda je 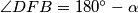 . Dakle,
. Dakle, 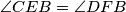 .
. 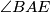 i
i 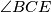 obodni kutovi u
obodni kutovi u  nad
nad 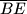 , onda je
, onda je 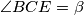 .
.  i
i 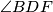 obodni kutovi u
obodni kutovi u  and
and 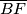 , onda je
, onda je 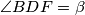 .
. 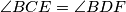 . Prema KK teoremu o sličnosti trokuta slijedi tvrdnja.
. Prema KK teoremu o sličnosti trokuta slijedi tvrdnja. 