Vrijeme: 01:53
KTT - primjer 1
Primjer 1. Neka su  i
i  središte opisane kružnice te ortocentar
središte opisane kružnice te ortocentar  redom.
redom.
Dokažite da 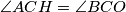 .
.
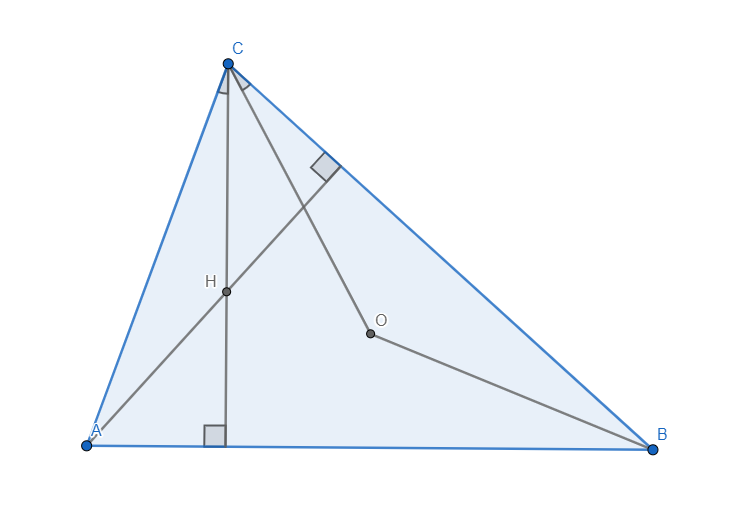
Rješenje:
Neka je 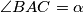 . Tada
. Tada 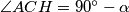 (iz pravokutnog trokuta sa vrhovima
(iz pravokutnog trokuta sa vrhovima 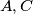 i nožište visine iz vrha
i nožište visine iz vrha  ). Budući da je
). Budući da je  središte opisane kružnice
središte opisane kružnice  , primjenom teorema o obodnom i središnjem kutu dobivamo
, primjenom teorema o obodnom i središnjem kutu dobivamo 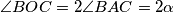 .
.
Također, 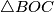 je jednakokračan budući da je
je jednakokračan budući da je 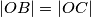 (polumjer opisane kružnice) te je tako
(polumjer opisane kružnice) te je tako 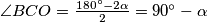 , čime smo dokazali tvrdnju zadatka.
, čime smo dokazali tvrdnju zadatka.
Za rješenje upiši broj pojavljivanja znaka jednakosti u ovom riješenom primjeru.
