Vrijeme: 01:57
KTT - primjer 2
Primjer 2: Neka su 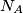 ,
, 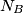 i
i 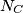 nožišta visina trokuta
nožišta visina trokuta  . Dokaži da je ortocentar trokuta
. Dokaži da je ortocentar trokuta  središte upisane kružnice
središte upisane kružnice 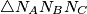 .
.
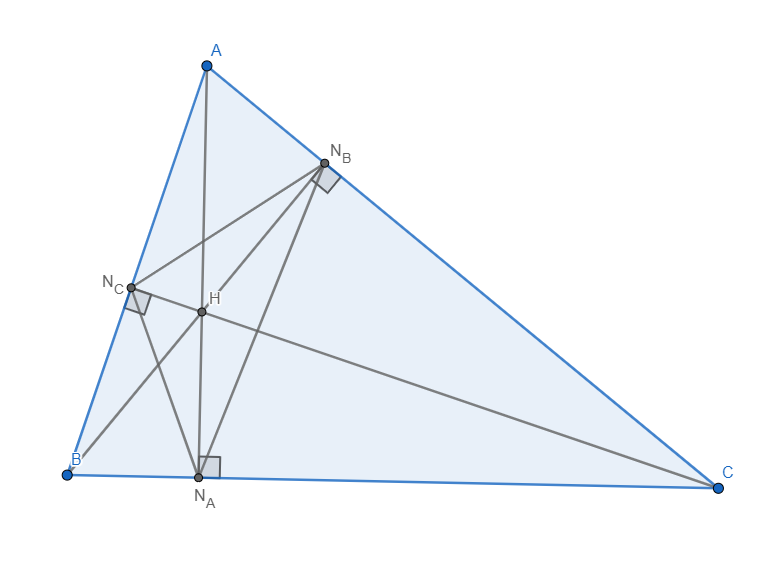
Rješenje:
Neka je  ortocentar trokuta
ortocentar trokuta  te standardno
te standardno 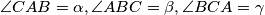 .
.
Budući da su 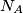 ,
,  i
i 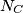 nožišta, slijedi da su
nožišta, slijedi da su 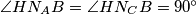 što znači da je četverokut
što znači da je četverokut 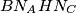 tetivan jer je zbroj nasuprotna dva kuta
tetivan jer je zbroj nasuprotna dva kuta 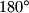 .
.
Iz tetivnosti sljedeći obodni kutevi su jednaki 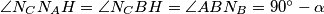 .
.
Slično, četverokut 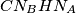 je tetivan te
je tetivan te 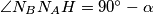 , što znači da je
, što znači da je 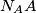 simetrala kuta
simetrala kuta 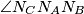 .
.
Analogno možemo dobiti da je 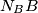 simetrala kuta
simetrala kuta 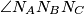 te
te 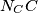 simetrala kuta
simetrala kuta  , što dokazuje da je
, što dokazuje da je  središte upisane kružnice trokuta
središte upisane kružnice trokuta 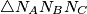 .
.
Za rješenje upišite  .
.
