Primjer 3: Dan je  . Neka su
. Neka su 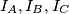 središta pripisanih kružnica nasuprot redom točaka
središta pripisanih kružnica nasuprot redom točaka 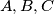 . Neka su dirališta pripisanih kružnica sa stranicama trokuta
. Neka su dirališta pripisanih kružnica sa stranicama trokuta 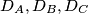 , ponovno redom nasuprot odgovarajućih vrhova. Dokažite da se
, ponovno redom nasuprot odgovarajućih vrhova. Dokažite da se 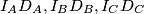 sijeku u jednoj točki (tj. da su konkurentni).
sijeku u jednoj točki (tj. da su konkurentni).
Rješenje:
Označimo standardno kuteve uz vrhove 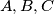 sa
sa 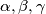 redom.
redom.
Lako je izračunati kuteve u trokutu 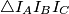 : budući da su
: budući da su 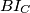 te
te 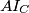 vanjske simetrale kuteva
vanjske simetrale kuteva  te
te  redom,
redom, 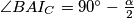 te
te 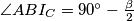 , pa slijedi da je
, pa slijedi da je  .
.
Analogno možemo dobiti 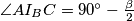 i
i 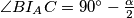 .
.
Presjecimo 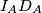 i
i 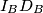 , neka je to točka
, neka je to točka  . Želimo dokazati da se
. Želimo dokazati da se  nalazi na pravcu
nalazi na pravcu 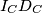 .
.
Kako su  i
i 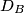 dirališta, kutevi
dirališta, kutevi 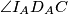 i
i 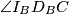 su pravi. Sada lako dobivamo
su pravi. Sada lako dobivamo  , što znači da se
, što znači da se  nalazi na simetrali
nalazi na simetrali  .
.
S druge strane, kako je  , pa iz leme (
, pa iz leme (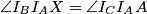 , zadatak xy.) slijedi da se središte opisane kružnice
, zadatak xy.) slijedi da se središte opisane kružnice 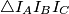 nalazi na
nalazi na 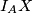 . Slično, dobivamo da se to isto središte nalazi i na pravcu
. Slično, dobivamo da se to isto središte nalazi i na pravcu 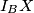 , iz čega zaključujemo da je
, iz čega zaključujemo da je  središte opisane kružnice trokuta
središte opisane kružnice trokuta 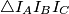 .
.
Sada možemo ponovno iskoristiti lemu kako bi dobili 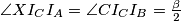 , a sličnim računom kao sa početka možemo dobiti i
, a sličnim računom kao sa početka možemo dobiti i 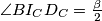 , što dokazuje tvrdnju zadatka pošto se
, što dokazuje tvrdnju zadatka pošto se 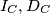 i
i  nalaze na istom pravcu.
nalaze na istom pravcu.
Ova točka se inače zove Bevanova točka  .
.
Za rješenje upišite koji je ovo broj primjera.
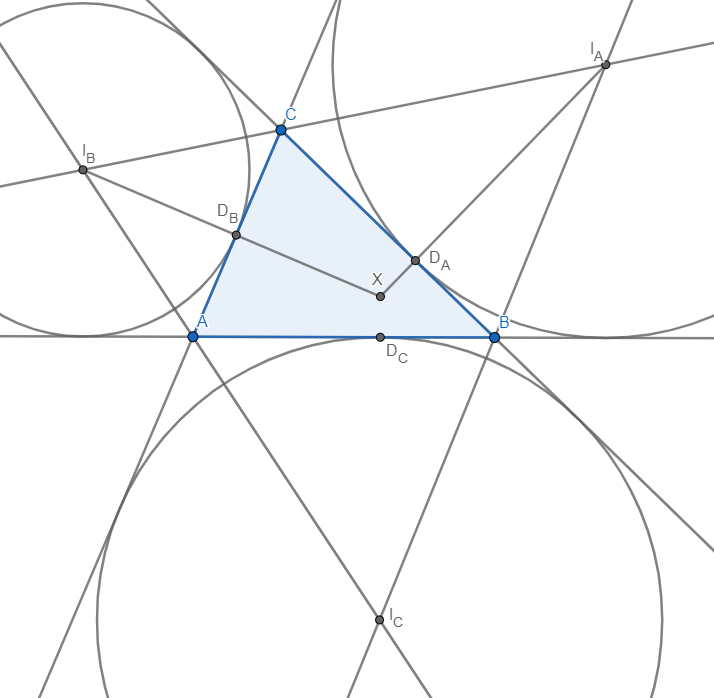
\textbf{Primjer 3:} Dan je $\triangle ABC$. Neka su $I_A, I_B, I_C$ središta pripisanih kružnica nasuprot redom točaka $A, B, C$. Neka su dirališta pripisanih kružnica sa stranicama trokuta $D_A, D_B, D_C$, ponovno redom nasuprot odgovarajućih vrhova. Dokažite da se $I_AD_A, I_BD_B, I_CD_C$ sijeku u jednoj točki (tj. da su konkurentni).
\includegraphics{bevan.png}
\textbf{Rješenje:}
Označimo standardno kuteve uz vrhove $A, B, C$ sa $\alpha, \beta, \gamma$ redom.
Lako je izračunati kuteve u trokutu $\triangle I_AI_BI_C$: budući da su $BI_C$ te $AI_C$ vanjske simetrale kuteva $\angle ABC$ te $\angle BAC$ redom, $\angle BAI_C = 90^\circ - \frac{\alpha}{2}$ te $\angle ABI_C = 90^\circ - \frac{\beta}{2}$, pa slijedi da je $\angle AI_CB = 90^\circ-\gamma$.
Analogno možemo dobiti $\angle AI_BC = 90^\circ - \frac{\beta}{2}$ i $\angle BI_AC = 90^\circ - \frac{\alpha}{2}$.
Presjecimo $I_AD_A$ i $I_BD_B$, neka je to točka $X$. Želimo dokazati da se $X$ nalazi na pravcu $I_CD_C$.
Kako su $D_A$ i $D_B$ dirališta, kutevi $\angle I_AD_AC$ i $\angle I_BD_BC$ su pravi. Sada lako dobivamo $\angle XI_AC=\angle XI_BC = \frac{\gamma}{2}$, što znači da se $X$ nalazi na simetrali $\overline{I_AI_B}$.
S druge strane, kako je $\angle I_CAI_A = 90^\circ \implies \angle I_CI_AA = \frac{\gamma}{2}$, pa iz leme ($\angle I_BI_AX = \angle I_CI_AA$, zadatak xy.) slijedi da se središte opisane kružnice $\triangle I_AI_BI_C$ nalazi na $I_AX$. Slično, dobivamo da se to isto središte nalazi i na pravcu $I_BX$, iz čega zaključujemo da je $X$ središte opisane kružnice trokuta $\triangle I_AI_BI_C$.
Sada možemo ponovno iskoristiti lemu kako bi dobili $\angle XI_CI_A = \angle CI_CI_B = \frac{\beta}{2}$, a sličnim računom kao sa početka možemo dobiti i $\angle BI_CD_C = \frac{\beta}{2}$, što dokazuje tvrdnju zadatka pošto se $I_C, D_C$ i $X$ nalaze na istom pravcu.
Ova točka se inače zove Bevanova točka $\triangle ABC$.
Za rješenje upišite koji je ovo broj primjera.
 . Neka su
. Neka su 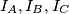 središta pripisanih kružnica nasuprot redom točaka
središta pripisanih kružnica nasuprot redom točaka 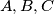 . Neka su dirališta pripisanih kružnica sa stranicama trokuta
. Neka su dirališta pripisanih kružnica sa stranicama trokuta 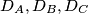 , ponovno redom nasuprot odgovarajućih vrhova. Dokažite da se
, ponovno redom nasuprot odgovarajućih vrhova. Dokažite da se 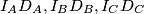 sijeku u jednoj točki (tj. da su konkurentni).
sijeku u jednoj točki (tj. da su konkurentni).
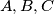 sa
sa 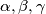 redom.
redom.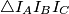 : budući da su
: budući da su 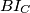 te
te 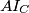 vanjske simetrale kuteva
vanjske simetrale kuteva  te
te  redom,
redom, 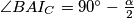 te
te 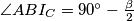 , pa slijedi da je
, pa slijedi da je  .
.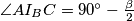 i
i 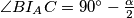 .
.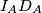 i
i 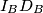 , neka je to točka
, neka je to točka  . Želimo dokazati da se
. Želimo dokazati da se  nalazi na pravcu
nalazi na pravcu 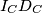 .
. i
i 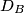 dirališta, kutevi
dirališta, kutevi 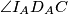 i
i 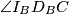 su pravi. Sada lako dobivamo
su pravi. Sada lako dobivamo  , što znači da se
, što znači da se  nalazi na simetrali
nalazi na simetrali  .
. , pa iz leme (
, pa iz leme (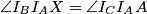 , zadatak xy.) slijedi da se središte opisane kružnice
, zadatak xy.) slijedi da se središte opisane kružnice 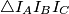 nalazi na
nalazi na 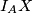 . Slično, dobivamo da se to isto središte nalazi i na pravcu
. Slično, dobivamo da se to isto središte nalazi i na pravcu 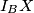 , iz čega zaključujemo da je
, iz čega zaključujemo da je  središte opisane kružnice trokuta
središte opisane kružnice trokuta 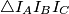 .
.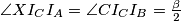 , a sličnim računom kao sa početka možemo dobiti i
, a sličnim računom kao sa početka možemo dobiti i 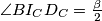 , što dokazuje tvrdnju zadatka pošto se
, što dokazuje tvrdnju zadatka pošto se 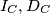 i
i  nalaze na istom pravcu.
nalaze na istom pravcu. .
.