Princip ekstrema - Primjer 2
Zadatak: U ravnini se nalazi konačno crvenih i plavih točaka. Na svakoj dužini čiji su krajevi crvene točke postoji plava točka, a na svakoj dužini čiji su krajevi plave točke, postoji crvena točka. Dokažite da sve točke leže na istom pravcu.
Rješenje:
Zadatak rješavamo metodom kontradikcije.
1. korak Pretpostavimo da nije istina da su u svakoj konfiguraciji koja zadovoljava uvjet sve točke na istom pravcu. To znači da postoji neka konfiguracija točaka koja zadovoljava traženi uvjet, a da sve točke ne leže na istom pravcu. Promotrimo jednu takvu konfiguraciju .
. 
 Primijetite da konfiguracija sa slike ne zadovoljava uvjet. Neka vas to ne zbunjuje - mi dokazujemo da i ne postoji konfiguracija nekolinearnih točaka koja ga zadovoljava. Prema konfiguraciji sa slike ćemo se ponašati kao da ga zadovoljava i koristeći to dokazati da na njoj mora vrijediti nešto očito pogrešno. Više o metodi kontradikcije možete saznati na sljedećem linku.
Primijetite da konfiguracija sa slike ne zadovoljava uvjet. Neka vas to ne zbunjuje - mi dokazujemo da i ne postoji konfiguracija nekolinearnih točaka koja ga zadovoljava. Prema konfiguraciji sa slike ćemo se ponašati kao da ga zadovoljava i koristeći to dokazati da na njoj mora vrijediti nešto očito pogrešno. Više o metodi kontradikcije možete saznati na sljedećem linku.
2. korak Kako sve točke ne leže na istom pravcu, neke od točaka sigurno tvore trokut. Promotrimo sve trokute koje tvore točke iz konfiguracije i promotrimo onaj najmanje površine.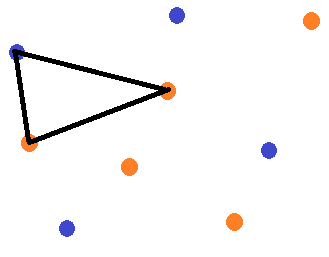
3. korak Taj trokut ima  vrha, a točke su obojene u
vrha, a točke su obojene u  boje, pa po Dirichletovom principu znamo da su neka
boje, pa po Dirichletovom principu znamo da su neka  vrha sigurno iste boje. Po uvjetu zadatka, na stranici trokuta čiji su vrhovi iste boje nalazi se točka suprotne boje.
vrha sigurno iste boje. Po uvjetu zadatka, na stranici trokuta čiji su vrhovi iste boje nalazi se točka suprotne boje. 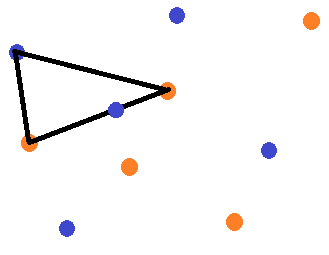
4. korak Trokut koji čine ta točka i bilo koja 2 vrha originalnog trokuta manje je površine nego originalni trokut, pa smo došli do kontradikcije i dokazali da tvrdnja ne vrijedi. 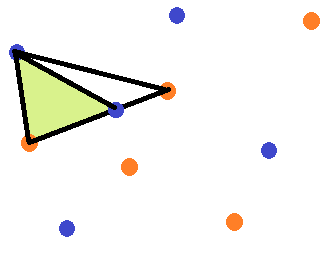
Kao rješenje upišite G.
