Zadatak: Pronađite sve prirodne brojeve 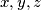 i
i  koji zadovoljavaju jednadžbu
koji zadovoljavaju jednadžbu 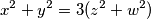
Rješenje:
Nakon što igrajući se i uvrštavajući razne vrijednosti ne uspijemo naći 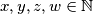 koji zadovoljavaju jednadžbu, naslutimo da rješenja nema. I ovaj zadatak rješavamo metodom kontradikcije - pretpostavimo da jednadžba ima barem jedno rješenje.
koji zadovoljavaju jednadžbu, naslutimo da rješenja nema. I ovaj zadatak rješavamo metodom kontradikcije - pretpostavimo da jednadžba ima barem jedno rješenje.
1. korak: Od svih rješenja, promotrimo one 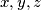 i
i  za koje je izraz
za koje je izraz 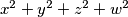 najmanji.
najmanji.
2. korak: Kako je desna strana jednadžbe djeljiva s  , mora biti i lijeva. Dakle, izraz
, mora biti i lijeva. Dakle, izraz 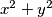 je djeljiv sa
je djeljiv sa  . Što to govori o
. Što to govori o  i
i  ?
?
Koliki uopće može biti ostatak pri dijeljenju potpunog kvadrata s tri? Prisjetimo li se 2. tjedna Metamath tečaja, nije teško zaključiti da je odgovor  ili
ili  .
.
Naime, prirodni broj  može davati ostatak
može davati ostatak  ,
,  ili
ili  pri dijeljenju s
pri dijeljenju s  :
:
- Ako  daje ostatak
daje ostatak  ,
,  daje ostatak
daje ostatak 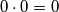 .
.
- Ako  daje ostatak
daje ostatak  ,
,  daje ostatak
daje ostatak 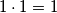 .
.
- Ako  daje ostatak
daje ostatak  ,
,  daje isti ostatak kao i
daje isti ostatak kao i 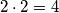 pri dijeljenju sa
pri dijeljenju sa  , dakle daje ostatak
, dakle daje ostatak  .
.
Vidimo da  i
i 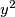 daju ostatke
daju ostatke  i
i  pri dijeljenju sa
pri dijeljenju sa  . Opet promatramo slučajeve:
. Opet promatramo slučajeve:
- Ako  i
i 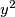 daju ostatak
daju ostatak  pri dijeljenju sa
pri dijeljenju sa  ,
, 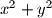 daje ostatak
daje ostatak 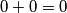 .
.
- Ako  daje ostatak
daje ostatak  , a
, a 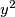 ostatak
ostatak  pri dijeljenju sa
pri dijeljenju sa  ili obratno,
ili obratno, 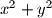 daje ostatak
daje ostatak 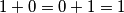 .
.
- Ako  i
i 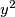 daju ostatak
daju ostatak  pri dijeljenju sa
pri dijeljenju sa  ,
, 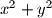 daje ostatak
daje ostatak 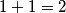 .
.
Dakle, 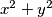 može biti djeljivo s
može biti djeljivo s  samo onda kad su i
samo onda kad su i  i
i 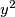 djeljivi s
djeljivi s  , a to se može dogoditi samo kad su
, a to se može dogoditi samo kad su  i
i  djeljivi s
djeljivi s  .
.
Ukoliko su vam ovakvi zaključci još uvijek pomalo strani, više zadataka za vježbu možete pronaći u MNM predavanjima Djeljivosti i Kongruencije.
Sada znamo da postoje 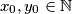 takvi da
takvi da 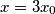 i
i 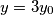 , pa jednadžba postaje
, pa jednadžba postaje 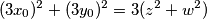
3. korak: Sređivanjem gornjeg izraza dobijemo jednadžbu 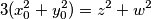 koju možemo napisati i kao
koju možemo napisati i kao 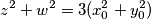 Primijetimo da to znači da su brojevi
Primijetimo da to znači da su brojevi  ,
,  ,
, 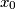 i
i 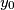 rješenja početne jednadžbe. Kako su
rješenja početne jednadžbe. Kako su 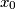 i
i 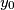 trećine od
trećine od  i
i  redom, znamo da vrijedi
redom, znamo da vrijedi 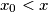 i
i 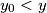 . Stoga
. Stoga 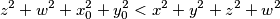 pa
pa 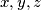 i
i  ne mogu biti takvi da je
ne mogu biti takvi da je 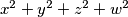 najmanji - došli smo do kontradikcije.
najmanji - došli smo do kontradikcije.
Kao rješenje upišite N.
\textbf{Zadatak:} Pronađite sve prirodne brojeve $x,y,z$ i $w$ koji zadovoljavaju jednadžbu
$$x^2+y^2 = 3(z^2+w^2)$$
\\\textbf{Rješenje:}
\\ Nakon što igrajući se i uvrštavajući razne vrijednosti ne uspijemo naći $x,y,z,w\in\mathbb{N}$ koji zadovoljavaju jednadžbu, naslutimo da rješenja nema.
I ovaj zadatak rješavamo \href{http://mnm.hr/wp-content/uploads/2015/10/sto_je_dokaz.pdf}{metodom kontradikcije} - pretpostavimo da jednadžba ima barem jedno rješenje.
\textbf{1. korak: } Od svih rješenja, promotrimo one $x,y,z$ i $w$ za koje je izraz $x^2+y^2+z^2+w^2$ najmanji.
\\\\\textbf{2. korak: } Kako je desna strana jednadžbe djeljiva s $3$, mora biti i lijeva.
Dakle, izraz $x^2 + y^2$ je djeljiv sa $3$. Što to govori o $x$ i $y$? \\
Koliki uopće može biti ostatak pri dijeljenju potpunog kvadrata s tri? Prisjetimo li se 2. tjedna Metamath tečaja, nije teško zaključiti da je odgovor $0$ ili $1$.
\\Naime, prirodni broj $a$ može davati ostatak $0$, $1$ ili $2$ pri dijeljenju s $3$: \\
- Ako $a$ daje ostatak $0$, $a^2$ daje ostatak $0\cdot 0 = 0$.
\\- Ako $a$ daje ostatak $1$, $a^2$ daje ostatak $1\cdot 1 = 1$.
\\- Ako $a$ daje ostatak $2$, $a^2$ daje isti ostatak kao i $2\cdot 2 = 4$ pri dijeljenju sa $3$, dakle daje ostatak $1$.
Vidimo da $x^2$ i $y^2$ daju ostatke $0$ i $1$ pri dijeljenju sa $3$. Opet promatramo slučajeve:\\
- Ako $x^2$ i $y^2$ daju ostatak $0$ pri dijeljenju sa $3$, $x^2+y^2$ daje ostatak $0 + 0 = 0$.
\\- Ako $x^2$ daje ostatak $1$, a $y^2$ ostatak $0$ pri dijeljenju sa $3$ ili obratno, $x^2+y^2$ daje ostatak $1+0=0+1 = 1$.
\\- Ako $x^2$ i $y^2$ daju ostatak $1$ pri dijeljenju sa $3$, $x^2+y^2$ daje ostatak $1 + 1 = 2$.
Dakle, $x^2 + y^2$ može biti djeljivo s $3$ samo onda kad su i $x^2$ i $y^2$ djeljivi s $3$, a to se može dogoditi samo kad su $x$ i $y$ djeljivi s $3$.
\\\\Ukoliko su vam ovakvi zaključci još uvijek pomalo strani, više zadataka za vježbu možete pronaći u MNM predavanjima \href{https://mnm.hr/wp-content/uploads/2015/10/djeljivosti.pdf}{Djeljivosti} i \href{https://mnm.hr/wp-content/uploads/2015/10/kongruencije.pdf}{Kongruencije}.
Sada znamo da postoje $x_0,y_0 \in \mathbb{N}$ takvi da $x = 3x_0$ i $y = 3y_0$, pa jednadžba postaje
$$(3x_0)^2+(3y_0)^2 = 3(z^2+w^2)$$
\\\textbf{3. korak: } Sređivanjem gornjeg izraza dobijemo jednadžbu
$$3(x_0^2+y_0^2) = z^2+w^2$$
koju možemo napisati i kao
$$z^2+w^2 = 3(x_0^2+y_0^2) $$
Primijetimo da to znači da su brojevi $z$, $w$, $x_0$ i $y_0$ rješenja početne jednadžbe. Kako su $x_0$ i $y_0$ trećine od $x$ i $y$ redom, znamo da vrijedi $x_0<x$ i $y_0<y$.
Stoga
$$z^2+w^2+x_0^2+y_0^2 < x^2+y^2+z^2+w^2$$
pa $x,y,z$ i $w$ ne mogu biti takvi da je $x^2+y^2+z^2+w^2$ najmanji - došli smo do kontradikcije.
\\\\
Kao rješenje upišite N.
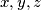 i
i  koji zadovoljavaju jednadžbu
koji zadovoljavaju jednadžbu 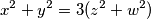
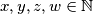 koji zadovoljavaju jednadžbu, naslutimo da rješenja nema. I ovaj zadatak rješavamo metodom kontradikcije - pretpostavimo da jednadžba ima barem jedno rješenje.
koji zadovoljavaju jednadžbu, naslutimo da rješenja nema. I ovaj zadatak rješavamo metodom kontradikcije - pretpostavimo da jednadžba ima barem jedno rješenje.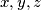 i
i  za koje je izraz
za koje je izraz 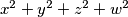 najmanji.
najmanji.  , mora biti i lijeva. Dakle, izraz
, mora biti i lijeva. Dakle, izraz 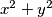 je djeljiv sa
je djeljiv sa  . Što to govori o
. Što to govori o  i
i  ?
?  ili
ili  .
.  može davati ostatak
može davati ostatak  ,
,  ili
ili  pri dijeljenju s
pri dijeljenju s  :
:  daje ostatak
daje ostatak  ,
,  daje ostatak
daje ostatak 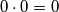 .
.  daje ostatak
daje ostatak  ,
,  daje ostatak
daje ostatak 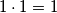 .
.  daje ostatak
daje ostatak  ,
,  daje isti ostatak kao i
daje isti ostatak kao i 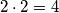 pri dijeljenju sa
pri dijeljenju sa  , dakle daje ostatak
, dakle daje ostatak  .
. i
i 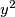 daju ostatke
daju ostatke  i
i  pri dijeljenju sa
pri dijeljenju sa  . Opet promatramo slučajeve:
. Opet promatramo slučajeve: i
i 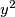 daju ostatak
daju ostatak  pri dijeljenju sa
pri dijeljenju sa  ,
, 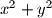 daje ostatak
daje ostatak 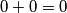 .
.  daje ostatak
daje ostatak  , a
, a 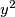 ostatak
ostatak  pri dijeljenju sa
pri dijeljenju sa  ili obratno,
ili obratno, 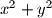 daje ostatak
daje ostatak 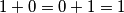 .
.  i
i 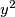 daju ostatak
daju ostatak  pri dijeljenju sa
pri dijeljenju sa  ,
, 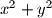 daje ostatak
daje ostatak 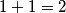 .
.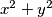 može biti djeljivo s
može biti djeljivo s  samo onda kad su i
samo onda kad su i  i
i 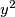 djeljivi s
djeljivi s  , a to se može dogoditi samo kad su
, a to se može dogoditi samo kad su  i
i  djeljivi s
djeljivi s  .
. 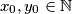 takvi da
takvi da 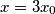 i
i 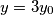 , pa jednadžba postaje
, pa jednadžba postaje 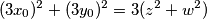
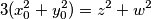 koju možemo napisati i kao
koju možemo napisati i kao 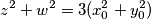 Primijetimo da to znači da su brojevi
Primijetimo da to znači da su brojevi  ,
,  ,
, 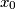 i
i 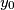 rješenja početne jednadžbe. Kako su
rješenja početne jednadžbe. Kako su 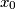 i
i 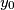 trećine od
trećine od  i
i  redom, znamo da vrijedi
redom, znamo da vrijedi 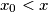 i
i 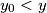 . Stoga
. Stoga 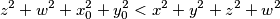 pa
pa 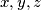 i
i  ne mogu biti takvi da je
ne mogu biti takvi da je 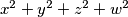 najmanji - došli smo do kontradikcije.
najmanji - došli smo do kontradikcije. 