\textbf{Zadatak:} Rješite sustav u skupu $\mathbb{R}$:
$$(y+z)^3 = x$$
$$ (z+x)^3=y$$
$$(x+y)^3 = z $$
\\\textbf{Rješenje:}
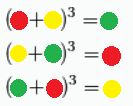
\\ Ključno je primijetiti da je zadani sustav \textbf{simetričan}, to jest da međusobnom zamjenom imena varijabli dobijamo iste jednadžbe.
\\
\begin{center}
\includegraphics{Zad31.png}
\end{center}
\\
Drugim riječima, kako god uvrstimo varijable $x,y,z$ kao boje crvena, žuta i zelena, dobijemo isti sustav. Ukoliko se prvi put susrećete s ovim pojmom, to zaista i napravite!
Zbog simetričnosti sustava bez smanjenja općenitosti smijemo pretpostaviti da je $x$ \textbf{najveći} od ta $3$ realna broja. Tada $x\geqslant y$, stoga raspisujemo
$$
\begin{aligned}
x&\geqslant y\\
(y+z)^3&\geqslant (z+x)^3 \quad \quad \quad\text{ Zašto smijemo uzeti treći korijen obje strane? }
\\ y+z&\geqslant z+x
\\ y &\geqslant x
\end{aligned}
$$
Dakle vrijedi $x \geqslant y$ i $y \geqslant x$, stoga $x = y$. Potpuno \href{http://mis.element.hr/fajli/507/03-02.pdf}{analogno} dobijemo i $x=z$, stoga mora biti $x = y = z$.
Uvrštavanjem $x = y = z$ jednadžba postaje
$$
\begin{aligned}
(x+x)^3 &= x\\
(2x)^3 &= x\\
8x^3 &= x\\
8x^3-x &= 0 \\
x(8x^2-1) &= 0 \quad \quad \quad \text{ Primijetimo razliku kvadrata} \\
x(2\sqrt2x-1)(2\sqrt2x+1) &= 0
\end{aligned}
$$
\\
Sada lako očitamo rješenja: $(0,0,0)$, $\left(\frac1{2\sqrt2},\frac1{2\sqrt2},\frac1{2\sqrt2}\right)$ i $\left(-\frac1{2\sqrt2},-\frac1{2\sqrt2},-\frac1{2\sqrt2}\right)$.
\\\\
Kao rješenje upišite A.
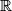 :
: 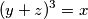
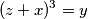
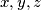 kao boje crvena, žuta i zelena, dobijemo isti sustav. Ukoliko se prvi put susrećete s ovim pojmom, to zaista i napravite!
kao boje crvena, žuta i zelena, dobijemo isti sustav. Ukoliko se prvi put susrećete s ovim pojmom, to zaista i napravite! najveći od ta
najveći od ta  realna broja. Tada
realna broja. Tada 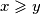 , stoga raspisujemo
, stoga raspisujemo 
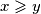 i
i 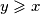 , stoga
, stoga 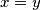 . Potpuno analogno dobijemo i
. Potpuno analogno dobijemo i  , stoga mora biti
, stoga mora biti 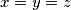 .
.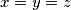 jednadžba postaje
jednadžba postaje 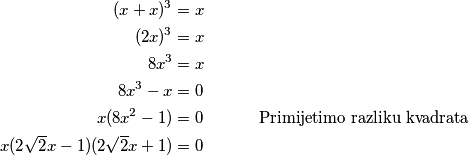
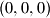 ,
, 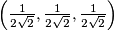 i
i 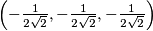 .
. 