MetaMath '22

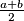\textbf{Zadatak:} $100$ realnih brojeva poredano je u krug na način da se između svaka $2$ broja $a$ i $b$ nalazi broj $\frac{a + b}2$. Dokažite da su svi brojevi u krugu jednaki. \\\textbf{Rješenje:} \\ Iskušajmo našu metodu. \\\textbf{1. Pretpostavimo suprotno:} Postoji konfiguracija takva da zadovoljava uvjet i svi brojevi u krugu nisu jednaki. \\ \\\textbf{2. Izdvojimo ekstrem:} Označimo najveći broj u tom krugu s $x$ \\\textbf{3. Nađimo ekstremnijeg:} $x$ je aritmetička sredina $2$ broja u krugu koja su mu susjedna, $a$ i $b$, takvi da je 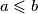$a\leqslant b$. Ako je 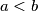$a<b$, vrijedi 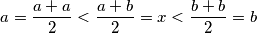$$a= \frac{a+a}2 < \frac{a+b}2 = x< \frac{b+b}2 = b$$ dakle u tom slučaju je $b$ veći od najvećeg broja u krugu, što je \textbf{kontradikcija} s izborom broja $x$. Zaključujemo da mora vrijediti 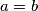$a = b$, pa je i 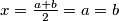$x = \frac{a+b}2 = a = b$, drugim riječima oba susjeda najvećeg broja u krugu su također jednaka najvećem broju u krugu. Sada isto možemo zaključiti i za njih, zatim za njihove susjede te susjede njihovih susjeda. 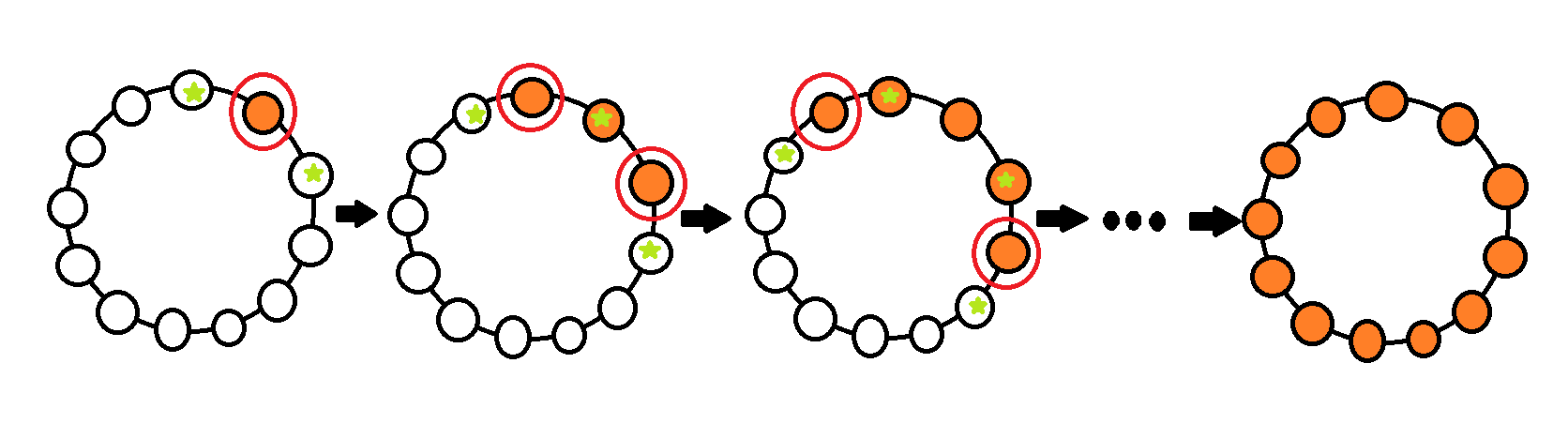\\ \includegraphics{Zad11.png} \\ Ponavljanjem tog postupka dobijemo da su svi brojevi u krugu jednaki $x$, što je u \href{http://mnm.hr/wp-content/uploads/2015/10/sto_je_dokaz.pdf}{kontradikciji} s odabirom kruga. Dakle, svi brojevi u krugu moraju biti jednaki - riješili smo zadatak! Kao rješenje upišite C.