Dobar dan i dobro nam došli na ovotjedni Metamath tečaj - ovaj put iz kombinatorike! Tema kojom se bavimo ovaj tjedan je Princip ekstrema - naučit ćemo da promatranjem toga što se događa s objektom koji je "naj" često možemo riješiti zadatak. Osnovnu ideju ćemo demonstrirati na tvrdnji koju smo dokazali ovdje u 2. tjednu tečaja:
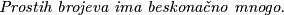
Važno je napomenuti da se ne može baš svaki zadatak uklopiti u sljedeći algoritam - promotriti objekt koji je po nekom svojstvu "naj" svejedno može biti korisno, stoga se ne ustručavajte pokušati i nešto drugačije. Krenimo na metodu:
1. Pretpostavimo suprotno: Princip ekstrema najčešće koristimo kao metodu kojom dokazujemo da nešto ne vrijedi. Dakle, prostih brojeva ima konačno mnogo.
2. Izdvojimo ekstrem: Promotrimo objekt koji je po nečemu "naj": najveći, najmanji, najudaljeniji, najslabiji... U težim zadacima zna ne biti očito po čemu to mjerimo elemente, stoga se nemojte ograničiti samo na manji/veći. U našem primjeru izdvojimo najveći prosti broj 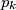 .
.
3. Nađimo ekstremnijeg: Srž principa ekstrema je pronaći objekt koji je više "naj" čak i od samog ekstrema: veći od najvećeg, manji od najmanjeg, dalji od najdaljeg, slabiji od najslabijeg... Takav objekt naravno ne postoji pa ukoliko ga pronađemo, dolazimo do kontradikcije. Što se tiče našeg primjera, broj 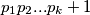 je prost i veći od najvećeg prostog broja
je prost i veći od najvećeg prostog broja 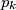 , pa smo došli do kontradikcije.
, pa smo došli do kontradikcije.
U ostatku lanca detaljno ćemo prokomentirati klasične primjere zadataka koji se mogu riješiti primjenom principa ekstrema, a više primjera i zadataka možete potražiti u MNM predavanju Princip ekstrema.
Kao rješenje upišite prezime gospodina koji je 2011. godine u kultnom šlageru opjevao objekt koji tražimo u 3. koraku naše metode (khm, hint).
Dobar dan i dobro nam došli na ovotjedni Metamath tečaj - ovaj put iz kombinatorike! Tema kojom se bavimo ovaj tjedan je Princip ekstrema - naučit ćemo da promatranjem toga što se događa s objektom koji je "naj" često možemo riješiti zadatak.
Osnovnu ideju ćemo demonstrirati na tvrdnji koju smo dokazali \href{https://www.skoljka.org/metamath22/task/1786/}{ovdje} u 2. tjednu tečaja:
\\$$\emph{Prostih brojeva ima beskonačno mnogo.} $$\\
Važno je napomenuti da se ne može baš svaki zadatak uklopiti u sljedeći algoritam - promotriti objekt koji je po nekom svojstvu "naj" svejedno može biti korisno, stoga se ne ustručavajte pokušati i nešto drugačije. Krenimo na metodu:
\\\\\textbf{1. Pretpostavimo suprotno:}
Princip ekstrema najčešće koristimo kao metodu kojom dokazujemo da nešto ne vrijedi. Dakle, prostih brojeva ima konačno mnogo.
\\\\
\textbf{2. Izdvojimo ekstrem:} Promotrimo objekt koji je po nečemu "naj": najveći, najmanji, najudaljeniji, najslabiji... U težim zadacima zna ne biti očito po čemu to mjerimo elemente, stoga se nemojte ograničiti samo na manji/veći. U našem primjeru izdvojimo najveći prosti broj $p_k$.
\\\\
\textbf{3. Nađimo ekstremnijeg:} \textbf{Srž principa ekstrema je pronaći objekt koji je više "naj" čak i od samog ekstrema}: veći od najvećeg, manji od najmanjeg, dalji od najdaljeg, slabiji od najslabijeg... Takav objekt naravno ne postoji pa ukoliko ga pronađemo, dolazimo do kontradikcije. Što se tiče našeg primjera, broj $p_1p_2...p_k+1$ je prost i veći od najvećeg prostog broja $p_k$, pa smo došli do kontradikcije.
\\
U ostatku lanca detaljno ćemo prokomentirati klasične primjere zadataka koji se mogu riješiti primjenom principa ekstrema, a više primjera i zadataka možete potražiti u MNM predavanju \href{https://mnm.hr/wp-content/uploads/2016/10/Princip_ekstrema.pdf}{Princip ekstrema}.
Kao rješenje upišite prezime gospodina koji je 2011. godine u kultnom šlageru opjevao objekt koji tražimo u 3. koraku naše metode (khm, \href{https://www.youtube.com/watch?v=RZjNm7mcpy8}{hint}).
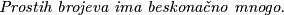
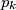 .
. 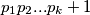 je prost i veći od najvećeg prostog broja
je prost i veći od najvećeg prostog broja 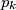 , pa smo došli do kontradikcije.
, pa smo došli do kontradikcije. 