MetaMath '22

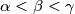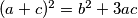\textbf{Primjer 1} Veličine kutova $\alpha<\beta<\gamma$ trokuta uzastopni su članovi aritmetičkog niza, a duljine njegovih stranica su $a,b,c$. Dokažite da vrijedi $(a+c)^2=b^2+3ac$. \textbf{Rješenje} Najprije ćemo malo preurediti jednakost koju trebamo dokazati. Imamo 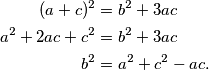$$\begin{aligned} (a+c)^2&=b^2+3ac\\ a^2+2ac+c^2&=b^2+3ac\\ b^2&=a^2+c^2-ac. \end{aligned}$$ Iz teorema o kosinusu znamo da u svakom trokutu vrijedi 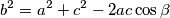$$b^2=a^2+c^2-2ac\cos\beta$$ pa uspoređujući zadanu jednakost s formulom gore zaključujemo da tvrdnja zadatka vrijedi ako i samo ako je 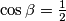$\cos\beta=\frac{1}{2}$. Kako je $\beta$ kut u trokutu slijedi da jednakost vrijedi ako i samo ako je $\beta=60$. 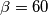Stoga ostaje dokazati da je 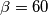$\beta=60$. Budući da u svakom aritmetičkom nizu 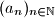$(a_n)_{n\in\mathbb{N}}$ za svaki 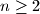$n\geq 2$ vrijedi 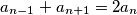$$a_{n-1}+a_{n+1}=2a_n$$ i jer su 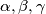$\alpha,\beta,\gamma$ uzastopni članovi aritmetičkog niza dobivamo da kutovi danog trokuta zadovoljavaju 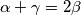$\alpha+\gamma=2\beta$. Iz ovog slijedi da je 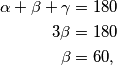$$\begin{aligned} \alpha+\beta+\gamma&=180\\ 3\beta&=180\\ \beta&=60, \end{aligned}$$ što smo i trebali dokazati. \textbf{Napomena}: Kao rješenje unesite $1$