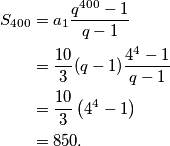Vrijeme: 03:07

Primjer 2: geometrijski niz

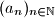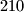Zadatak Neka je (a_n)_{n\in\mathbb{N}} geometrijski niz. Ukoliko je zbroj prvih sto članova tog niza jednak 10, a zbroj prvih tristo članova tog niza jednak 210, koliki je zbroj prvih četiristo članova tog niza?

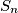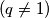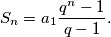
Rješenje Označimo sa q kvocijent danog niza, a sa S_n sumu prvih n članova niza. Ukoliko niz nije konstantan (q\neq 1), zbroj prvih n članova geometrijskog niza dan je S_n=a_1\frac{q^n-1}{q-1}.

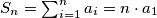Činjenicu da dani niz nije konstantan dokazujemo na sljedeći način: pretpostavimo da jest konstantan. Tada je zbroj prvih n članova S_{n}=\sum_{i=1}^n a_i=n\cdot a_1. Iz teksta zadatka imamo da je 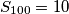S_{100}=10 iz čega dobivamo da je 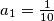a_1=\frac{1}{10}, a iz 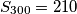S_{300}=210 dobivamo da je 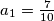a_1=\frac{7}{10}. To nije moguće. Dakle dani niz nije konstantan.

Dakle je 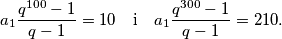a_1\frac{q^{100}-1}{q-1}=10\quad\text{i}\quad a_1\frac{q^{300}-1}{q-1}=210. Dijeljenjem druge jednakosti s prvom dobivamo 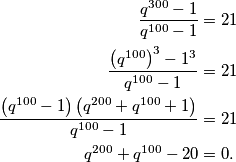\begin{aligned} \frac{q^{300}-1}{q^{100}-1}&=21\\ \frac{\left(q^{100}\right)^3-1^3}{q^{100}-1}&=21\\ \frac{\left(q^{100}-1\right)\left(q^{200}+q^{100}+1\right)}{q^{100}-1}&=21\\ q^{200}+q^{100}-20&=0. \end{aligned} Uvedemo li supstituciju 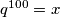q^{100}=x dobivamo kvadratnu jednadžbu 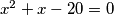x^2+x-20=0. 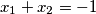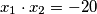Vieteove formule daju x_1+x_2=-1 i x_1\cdot x_2=-20 iz čega lako vidimo da su rješenja 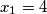x_1=4 i x_2=-5. 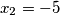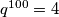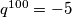Vraćanjem supstitucije slijedi da je q^{100}=4 i q^{100}=-5. 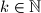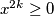Budući da za svaki realan broj x i za svaki k\in\mathbb{N} imamo x^{2k}\geq 0, rješenje 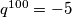q^{100}=-5 možemo odbaciti. 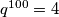Dakle, jedina mogućnost je q^{100}=4.

Uvrštavanjem dobivenog u formulu za 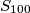S_{100} dobivamo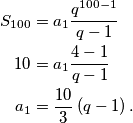 \begin{aligned} S_{100}&=a_1\frac{q^{100-1}}{q-1}\\ 10&=a_1\frac{4-1}{q-1}\\ a_1&=\frac{10}{3}\left(q-1\right). \end{aligned}

Sada računamo traženu sumu \begin{aligned} S_{400}&=a_1\frac{q^{400}-1}{q-1}\\ &=\frac{10}{3}(q-1)\frac{4^4-1}{q-1}\\ &=\frac{10}{3}\left(4^4-1\right)\\ &=850. \end{aligned}