MetaMath '22

\textbf{Zadatak} Niz brojeva definiran je s 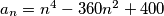$a_n=n^4-360n^2+400$. Izračunajte zbroj svih članova tog niza koji su prosti brojevi. \textbf{Rješenje} Zbog izgleda općeg člana slutimo da bi se isti trebao dati faktorizirati, pa ćemo najprije to i (pokušati) napraviti. Imamo 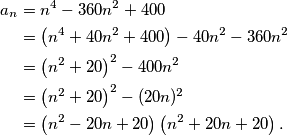$$\begin{aligned} a_n&=n^4-360n^2+400\\ &=\left(n^4+40n^2+400\right)-40n^2-360n^2 \\ &=\left(n^2+20\right)^2-400n^2\\ &=\left(n^2+20\right)^2-(20n)^2\\ &=\left(n^2-20n+20\right)\left(n^2+20n+20\right). \end{aligned}$$ Broj $a_n$ je prost ako i samo je jedan od gornja dva faktora jednaka $1$ i ako je drugi faktor prost broj. Ako je 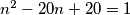$n^2-20n+20=1$ tada dobivamo kvadratnu jednadžbu 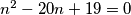$n^2-20n+19=0$. 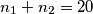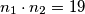Primjenom Vieteovih formula dobivamo da rješenja zadovoljavaju $n_1+n_2=20$ i $n_1\cdot n_2=19$ iz čega se lako vidi da su rješenja 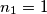$n_1=1$ i $n_2=19$. 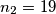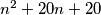Sada trebamo provjeritidobivamo li uvrštavanjem brojeva $1$ i $19$ u $n^2+20n+20$ prost broj. 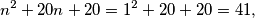Za $n=1$ imamo $$\begin{aligned} n^2+20n+20=1^2+20+20=41, \end{aligned}$$ što jest prost broj. Za 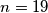$n=19$ dobivamo 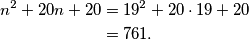$$\begin{aligned} n^2+20n+20&=19^2+20\cdot19+20\\ &=761. \end{aligned}$$ Lako se ručno provjeri da je taj broj prost (sjetimo se da je dovoljno provjeriti da ga ne dijeli niti jedan prost broj manji ili jednak 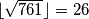$\lfloor\sqrt{761}\rfloor=26$, odnosno da ga ne dijele brojevi 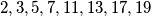$2,3,5,7,11,13,17,19$ i $23$). 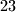Ako pak je 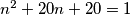$n^2+20n+20=1$ tada dobivamo kvadratnu jednadžbu 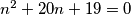$n^2+20n+19=0$. 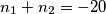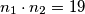Vieteove formule nam daju $n_1+n_2=-20$ i $n_1\cdot n_2=19$ iz čega se lako vidi da su rješenja 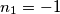$n_1=-1$ i $n_2=-19$. 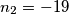Kako su oba broja negativna u ovom slučaju nemamo rješenja. 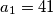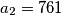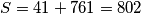Zaključujemo da su jedini članovi tog niza koji su prosti brojevi $a_1=41$ i $a_2=761$ pa je rješenje $S=41+761=802$.