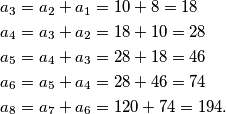\textbf{Zadatak} Neka je $(a_n)$ niz pozitivnih cijelih brojeva takav da vrijedi
$$a_1< a_2\quad\text{i}\quad a_{n+2}=a_{n+1}+a_{n},\quad n\geq 1.$$
Ako je $a_7=120$, koliko je $a_8$?
\textbf{Rješenje}
Korištenjem rekurzivne relacije dobivamo da je
$$\begin{aligned}
120&=a_7\\
&=a_6+a_5=2a_5+a_4=3a_4+2a_3=5a_3+3a_2=8a_2+5a_1.
\end{aligned}$$
Slijedi da je
$$\begin{aligned}
a_2&=\frac{120-5a_1}{8}\\
&=15-\frac{5}{8}a_1.
\end{aligned}$$
Iz ovog zaključujemo da je $a_2$ cijeli broj samo ako i samo ako je $a_1$ oblika $8k,\;k\in\mathbb{N}$.
Za $k=1$ dobivamo $a_1=8$ i $a_2=15-5=10$. Za $k=2$ dobivamo $a_1=16$ i $a_2=15-10=5$. Budući da nam je u zadatku zadano da je $a_2>a_1$ drugo rješenje odbacujemo. Za $k\geq 3$ je $a_2\leq 0$ pa zaključujemo da je jedino rješenje $a_1=8$ i $a_2=10$.
Sada dobivamo
$$\begin{aligned}
a_3&=a_2+a_1=10+8=18\\
a_4&=a_3+a_2=18+10=28\\
a_5&=a_4+a_3=28+18=46\\
a_6&=a_5+a_4=28+46=74\\
a_8&=a_7+a_6=120+74=194.
\end{aligned}$$
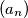 niz pozitivnih cijelih brojeva takav da vrijedi
niz pozitivnih cijelih brojeva takav da vrijedi 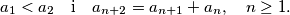 Ako je
Ako je 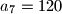 , koliko je
, koliko je 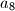 ?
?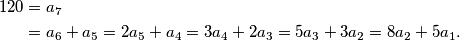 Slijedi da je
Slijedi da je 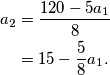 Iz ovog zaključujemo da je
Iz ovog zaključujemo da je  cijeli broj samo ako i samo ako je
cijeli broj samo ako i samo ako je  oblika
oblika 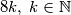 . Za
. Za 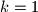 dobivamo
dobivamo 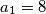 i
i 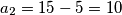 . Za
. Za 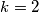 dobivamo
dobivamo  i
i 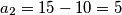 . Budući da nam je u zadatku zadano da je
. Budući da nam je u zadatku zadano da je  drugo rješenje odbacujemo. Za
drugo rješenje odbacujemo. Za 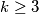 je
je 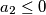 pa zaključujemo da je jedino rješenje
pa zaključujemo da je jedino rješenje 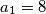 i
i 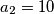 .
.