MetaMath '22

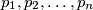\textbf{Zadatak} Neka je u ravnini dano $n$ pravaca $p_1, p_2, \ldots, p_n$ u općem položaju (nikoja tri pravca ne prolaze istom točkom i nema paralelnih pravaca). Označimo sa 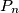$P_n$ broj dijelova ravnine na koje ti pravci dijele ravninu. Odredite opći član niza 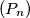$(P_n)$. \textbf{Rješenje} Promatrajmo broj dijelova 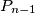$P_{n-1}$ na koje 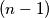$(n-1)$ pravac ravnine 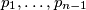$p_1,\ldots,p_{n-1}$ dijeli ravninu i $n$-ti pravac $p_n$. 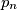Dodavanjem tog pravca broj dijelova 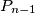$P_{n-1}$ povećava se za $n$. 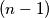Naime, broj novonastalih dijelova odgovara broju dijelova što ga $(n-1)$ pravac određuje na $n$-tom pravcu. Budući da su svi u općem položaju, tih dijelova ima $n$. Po gornjoj diskusiji zaključujemo da za 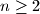$n\geq 2$ vrijedi 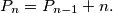$$P_n=P_{n-1}+n.$$ Zbrajanjem prvih 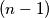$(n-1)$ članova bez prvog člana 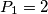$P_1=2$ tog niza dobivamo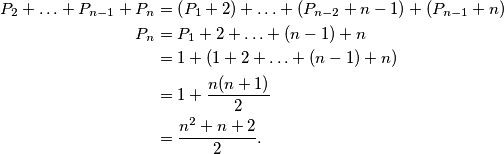 $$\begin{aligned} P_2+\ldots+P_{n-1}+P_n&=\left(P_1+2\right)+\ldots+\left(P_{n-2}+n-1\right)+\left(P_{n-1}+n\right)\\ P_n&=P_1+2+\ldots+(n-1)+n\\ &=1+(1+2+\ldots+(n-1)+n)\\ &=1+\frac{n(n+1)}{2}\\ &=\frac{n^2+n+2}{2}. \end{aligned}$$ \textbf{Napomena}: Za rješenje unesite $1$.