Primjer 6: indukcija
Zadatak: Neka je 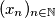 čiji članovi zadovoljavaju rekurzivnu formulu
čiji članovi zadovoljavaju rekurzivnu formulu 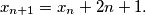 Ukoliko je prvi član niza jednak
Ukoliko je prvi član niza jednak  dokažite da je
dokažite da je 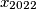 djeljiv s
djeljiv s 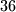 .
.
Rješenje Primjetimo specifičnost rekurzije koja je zadana. Ukoliko bi umjesto 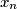 pisalo
pisalo 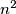 imalo bismo da je
imalo bismo da je 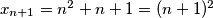 , dakle i za
, dakle i za 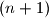 -vi član niza bismo dobili da je jednak kvadratu svojeg rednog broja. Dakle, slutimo da je zadani niz zapravo niz kvadrata prirodnih brojeva, odnosno
-vi član niza bismo dobili da je jednak kvadratu svojeg rednog broja. Dakle, slutimo da je zadani niz zapravo niz kvadrata prirodnih brojeva, odnosno 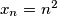 . Ukoliko to pokažemo tada iz
. Ukoliko to pokažemo tada iz 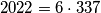 dobivamo
dobivamo 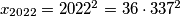 iz čega slijedi
iz čega slijedi  .
.
Činjenicu da je 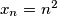 možemo dobiti na dva načina: ili ju korištenjem dane rekurzije dobijemo direktno (takozvani "glavom-kroz-zid" pristup ili "gruba sila"; najčešće treba zbrojiti neke članove tog niza) ili ju dokažemo korištenjem principa matematičke indukcije.
možemo dobiti na dva načina: ili ju korištenjem dane rekurzije dobijemo direktno (takozvani "glavom-kroz-zid" pristup ili "gruba sila"; najčešće treba zbrojiti neke članove tog niza) ili ju dokažemo korištenjem principa matematičke indukcije.
Gruba sila
Ukoliko u rekurzivno zadanom nizu sljedeći član niza na jednostavan način ovisi o prethodnom često se isplati zbrojiti prvih  članova niza
članova niza ![\begin{aligned}
x_1+x_2+\ldots+x_n&=1+(x_1+2\cdot 1+1)+(x_2+2\cdot 2+1)+\ldots+\left[x_{n-1}+2\cdot(n-1)+1\right]\\
&=(x_1+x_2+\ldots+x_{n-1})+[2\cdot1+2\cdot2+\ldots+2\cdot(n-1)]+(\underbrace{1+1+\ldots+1}_{n-\text{puta}})\\
&=(x_1+x_2+\ldots x_{n-1})+2[1+2+\ldots+(n-1)]+n.
\end{aligned}](/media/m/9/d/e/9defbe87cb730032a5273344516597b6.png) Slijedi da je
Slijedi da je  -ti član niza jednak
-ti član niza jednak ![x_n=2[1+2+\ldots+(n-1)]+n.](/media/m/5/9/0/590b493ad410def3578b360df59cbc74.png) Primjetimo da u zagradi imamo sumu prvih
Primjetimo da u zagradi imamo sumu prvih 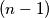 prirodnih brojeva. Budući da je suma prvih
prirodnih brojeva. Budući da je suma prvih  prirodnih brojeva jednaka
prirodnih brojeva jednaka 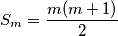 slijedi da je
slijedi da je 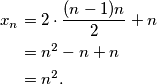
Korištenje principa matematičke indukcije
Tvrdimo da za svaki prirodan broj  vrijedi
vrijedi 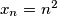 .
.
![\begin{enumerate}
\item[\textbf{Baza indukcije}:]
Uvrštavanjem $n=1$ dobivamo $x_1=n^2=1^2=1$ za što iz teksta zadatka znamo da vrijedi.
\item[\textbf{Pretpostavka indukcije}:]
Pretpostavimo da tvrdnja vrijedi za neki prirodan broj $n$, dakle
$x_n=n^2$.
\item[\textbf{Korak indukcije}:]
Dokažimo da tada tvrdnja vrijedi i za sljedeći prirodan broj, $n+1$.
Iz formule rekurzije imamo da je $x_{n+1}=x_n+2n+1$, pa uvrštavanjem jednakosti iz pretpostavke indukcije dobivamo da je $$x_{n+1}=n^2+2n+1=(n+1)^2,$$ što smo i trebali dokazati.
\end{enumerate}](/media/m/6/2/3/6238ac446bb19561580bd18e80190f3c.png) Po principu matematičke indukcije slijedi da tvrdnja vrijedi za svaki prirodan broj
Po principu matematičke indukcije slijedi da tvrdnja vrijedi za svaki prirodan broj  .
.
Napomena: Kao rješenje unesite  .
.
