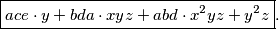Ovaj tjedan bavit ćemo se polinomima. Prije svega, ispričajmo što su oni i zašto se uopće bavimo njima.
DISCLAIMER: Sve što slijedi moja je misaona igra i slobodna interpretacija nekih općepoznatih pojmova, pa sve primite s otvorenim umom i kojim zrnom soli.
Vratimo se skroz na početak, u početne razrede osnovne škole. Tada smo svi smatrali da je cijela matematika samo igra s brojevima. Sami broj tada percipiramo kao elementarni i iskonski pojam koji postoji ,,sam od sebe'', ničim uvjetovan i ni o čemu zavisan, slično kao što su kemičari i fizičari doživljavali atome prije otkrića elementarnih čestica i ostalih čudesa moderne fizike. To govori o ukorijenjenosti pojma broja u našem intuitivnom poimanju (apstraktne) stvarnosti.
Nadalje, uz broj je nerazdvojimo vezan pojam brojanja - možemo reći da su u sličnoj vezi kao kokoš i jaje. U svakom slučaju (po)imamo brojeve i brojanje. Time stječemo dojam ,,fluidnosti'' brojeva: oni se pretvaraju jedni u druge, međusobno su povezani i izmjenjivi. Brojeve ,,nabrajamo'' sa zarezom:  ,
,  ,
,  ; ne odvajamo ih točkom:
; ne odvajamo ih točkom:  .
.  .
.  .
.
U pozadini brojanja je dodavanje. Svaki sljedeći broj u nizu dobiven je dodavanjem jedne jedinice više prethodnom.  je zapravo
je zapravo  i
i  , a
, a  ništa drugo nego
ništa drugo nego  i
i  i još
i još  . Broj je zapravo više jedinica. Dodavanje jedinica je brojanje. Kokoš i jaje.
. Broj je zapravo više jedinica. Dodavanje jedinica je brojanje. Kokoš i jaje.
Sada, jednim malim korakom za čovjeka, a velikim za čovječanstvom, snaga naše apstraktne misli omogućila nam je da poopćimo ovaj primitivni postupak na prvu pravu operaciju s brojevima. Trik se sastoji od sljedećeg: umjesto jedne jedinice, početnom broju možemo dodati više jedinica odjednom. Ovo ,,više jedinica odjednom'' je prema prethodnom paragragfu ustvari broj. Dakle, početnom broju dodajemo ne više jedinicu, nego broj. Eureka, zbrajanje je rođeno!
Zbrajanje je dakle osnovna operacija s brojevima, direktno proizašla iz procesa brojanja. Zbrajanje je toliko često i uobičajeno korišteno, da su ljudi dalje razvijali tehnike za brže i efikasnije provođenje ove operacije. S vremenom se tako iskristariziralo sažimanje višestrukog zbrajanja u operaciju svima nam poznatu kao množenje.
Zbrajanje i množenje najjednostavnije su operacije s brojevima, svepristune u životu prosječnog stanovnika današnje Zemlje. Mi znamo i za potenciranje kao skraćeno množenje, ali ono nije toliko prisutno u svakodnevnom životu, osim ako su dio obrazovanja ili struke.
Pomalo dolazimo do poante ovog filozofiranja. Dakle, imamo brojeve koje možemo jednostavno zbrajati i množiti. Što nam to formalno ,,daje'', u terminima algebre? U prvom tjednu imali ste priliku proučavati razne algebarske izraze i njihova svojstva. Usredotočimo se ovdje na algebarske izraze koji nastaju jedino konačnom primjenom operacija zbrajanja i množenja. Što možemo ,,napraviti'' u ovakvom okruženju? Neka su brojevi koje uzimamo kao operande označeni slovima s početka abecede:  ,
,  ,
,  ,
,  Primjetimo da još ne govorimo o varijablama - brojeve koje uzmemo su fiksni, ali još neodređeni. Zovemo ih parametri.
Primjetimo da još ne govorimo o varijablama - brojeve koje uzmemo su fiksni, ali još neodređeni. Zovemo ih parametri.  je uvijek jedan fiksni broj, ali proizvoljno odabran. Dakle, možemo dobiti ovakve izraze:
je uvijek jedan fiksni broj, ali proizvoljno odabran. Dakle, možemo dobiti ovakve izraze: 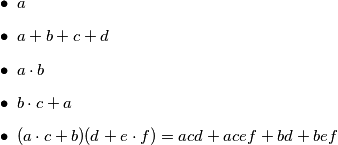
Ovaj zadnji izraz daje nam za naslutiti općeniti oblik izraza kojeg možemo dobiti s ovim ograničenim fondom operacija. Za sada, dobili smo neke izraze, ali ne posebno korisne: svaki od njih svede se na jedan rezultirajući broj nakon uvrštavanja vrijednosti parametara. To znači da ovim postupkom možemo dobiti jedino jednostavne zadatke izračunavanja izraza, što i nije posebno uzbudljivo niti zanimljivo.
Pravu stvar dobijemo kada dopustimo uvođenje još jednog specijalnog ,,parametra'' koji nije fiksan. Ovakvi parametri zovu se varijable. Označavamo ih slovima s kraja abecede:  (evo ga!),
(evo ga!),  ,
,  ,
,  . Sada dobijemo izraze slične sljedećem:
. Sada dobijemo izraze slične sljedećem: 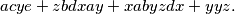 Nakon uobičajenom grupiranja (parametri na početak, varijable na kraj, hvala komutativnosti) i uvođenja potencija samo u svrhu sažetijeg zapisivanja, dobijemo sljedeći uređeni izraz:
Nakon uobičajenom grupiranja (parametri na početak, varijable na kraj, hvala komutativnosti) i uvođenja potencija samo u svrhu sažetijeg zapisivanja, dobijemo sljedeći uređeni izraz: 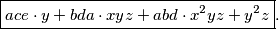
Time smo konačno stigli do našeg prvog polinoma!!!
Huh, dosta za prvi susret s polinomima. Nastavak slijedi. Kao rješenje upišite od koliko se monoma sastoji naš polinom (više detalja o ovim imenima u nastavku, ali znam da već znate).
Ovaj tjedan bavit ćemo se \textbf{polinomima}. Prije svega, ispričajmo što su oni i zašto se uopće bavimo njima.
\emph{DISCLAIMER: Sve što slijedi moja je misaona igra i slobodna interpretacija nekih općepoznatih pojmova, pa sve primite s otvorenim umom i kojim zrnom soli.}
Vratimo se skroz na početak, u početne razrede osnovne škole. Tada smo svi smatrali da je cijela matematika samo igra s brojevima. Sami \emph{broj} tada percipiramo kao elementarni i iskonski pojam koji postoji ,,sam od sebe'', ničim uvjetovan i ni o čemu zavisan, slično kao što su kemičari i fizičari doživljavali atome prije otkrića elementarnih čestica i ostalih čudesa moderne fizike. To govori o ukorijenjenosti pojma broja u našem intuitivnom poimanju (apstraktne) stvarnosti.
Nadalje, uz broj je nerazdvojimo vezan pojam \emph{brojanja} - možemo reći da su u sličnoj vezi kao kokoš i jaje. U svakom slučaju (po)imamo brojeve i brojanje. Time stječemo dojam ,,fluidnosti'' brojeva: oni se pretvaraju jedni u druge, međusobno su povezani i izmjenjivi. Brojeve ,,nabrajamo'' sa zarezom: $1$, $2$, $3$; ne odvajamo ih točkom: $1$. $2$. $3$.
U pozadini brojanja je \emph{dodavanje}. Svaki sljedeći broj u nizu dobiven je dodavanjem jedne jedinice više prethodnom. $2$ je zapravo $1$ i $1$, a $3$ ništa drugo nego $1$ i $1$ i još $1$. \emph{Broj} je zapravo \emph{više jedinica}. Dodavanje jedinica je \emph{brojanje}. Kokoš i jaje.
Sada, jednim malim korakom za čovjeka, a velikim za čovječanstvom, snaga naše apstraktne misli omogućila nam je da poopćimo ovaj primitivni postupak na prvu pravu \textbf{operaciju} s brojevima. Trik se sastoji od sljedećeg: umjesto jedne jedinice, početnom broju možemo dodati više jedinica odjednom. Ovo ,,više jedinica odjednom'' je prema prethodnom paragragfu ustvari broj. Dakle, početnom broju dodajemo ne više jedinicu, nego \emph{broj}. Eureka, \textbf{zbrajanje} je rođeno!
Zbrajanje je dakle osnovna operacija s brojevima, direktno proizašla iz procesa brojanja. Zbrajanje je toliko često i uobičajeno korišteno, da su ljudi dalje razvijali tehnike za brže i efikasnije provođenje ove operacije. S vremenom se tako iskristariziralo sažimanje višestrukog zbrajanja u operaciju svima nam poznatu kao \emph{množenje}.
Zbrajanje i množenje najjednostavnije su operacije s brojevima, svepristune u životu prosječnog stanovnika današnje Zemlje. Mi znamo i za potenciranje kao skraćeno množenje, ali ono nije toliko prisutno u svakodnevnom životu, osim ako su dio obrazovanja ili struke.
Pomalo dolazimo do poante ovog filozofiranja. Dakle, imamo brojeve koje možemo jednostavno zbrajati i množiti. Što nam to formalno ,,daje'', u terminima \textbf{algebre}? U prvom tjednu imali ste priliku proučavati razne algebarske izraze i njihova svojstva. Usredotočimo se ovdje na algebarske izraze koji nastaju jedino konačnom primjenom operacija zbrajanja i množenja. Što možemo ,,napraviti'' u ovakvom okruženju? Neka su brojevi koje uzimamo kao operande označeni slovima s početka abecede: $a$, $b$, $c$, $\dots$ Primjetimo da još ne govorimo o \emph{varijablama} - brojeve koje uzmemo su fiksni, ali još neodređeni. Zovemo ih \emph{parametri}. $a$ je uvijek jedan fiksni broj, ali proizvoljno odabran. Dakle, možemo dobiti ovakve izraze:
\begin{itemize}
\item $a$
\item $a + b + c + d$
\item $a \cdot b$
\item $b \cdot c + a$
\item $(a \cdot c + b)(d + e \cdot f) = acd + acef + bd + bef$
\end{itemize}
Ovaj zadnji izraz daje nam za naslutiti općeniti oblik izraza kojeg možemo dobiti s ovim ograničenim fondom operacija. Za sada, dobili smo neke izraze, ali ne posebno korisne: svaki od njih svede se na jedan rezultirajući broj nakon uvrštavanja vrijednosti parametara. To znači da ovim postupkom možemo dobiti jedino jednostavne zadatke izračunavanja izraza, što i nije posebno uzbudljivo niti zanimljivo.
Pravu stvar dobijemo kada dopustimo uvođenje još jednog specijalnog ,,parametra'' koji \textbf{nije fiksan}. Ovakvi parametri zovu se \emph{varijable}. Označavamo ih slovima s kraja abecede: $x$ (evo ga!), $y$, $z$, $\dots$. Sada dobijemo izraze slične sljedećem:
$$ acye + zbdxay + xabyzdx + yyz.$$
Nakon uobičajenom grupiranja (parametri na početak, varijable na kraj, hvala komutativnosti) i uvođenja potencija \underline{samo u svrhu sažetijeg zapisivanja}, dobijemo sljedeći uređeni izraz:
$$ \boxed{ace\cdot y + bda\cdot xyz + abd\cdot x^2yz + y^2z}.$$
Time smo konačno stigli do našeg prvog \textbf{polinoma}!!!
Huh, dosta za prvi susret s polinomima. Nastavak slijedi. Kao rješenje upišite od koliko se \emph{monoma} sastoji naš polinom (više detalja o ovim imenima u nastavku, ali znam da već znate).
 ,
,  ,
,  ; ne odvajamo ih točkom:
; ne odvajamo ih točkom:  .
.  .
.  .
. je zapravo
je zapravo  i
i  , a
, a  ništa drugo nego
ništa drugo nego  i
i  i još
i još  . Broj je zapravo više jedinica. Dodavanje jedinica je brojanje. Kokoš i jaje.
. Broj je zapravo više jedinica. Dodavanje jedinica je brojanje. Kokoš i jaje. ,
,  ,
,  ,
,  Primjetimo da još ne govorimo o varijablama - brojeve koje uzmemo su fiksni, ali još neodređeni. Zovemo ih parametri.
Primjetimo da još ne govorimo o varijablama - brojeve koje uzmemo su fiksni, ali još neodređeni. Zovemo ih parametri.  je uvijek jedan fiksni broj, ali proizvoljno odabran. Dakle, možemo dobiti ovakve izraze:
je uvijek jedan fiksni broj, ali proizvoljno odabran. Dakle, možemo dobiti ovakve izraze: 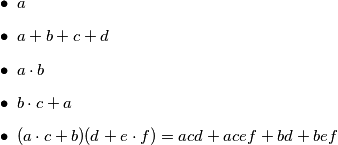
 (evo ga!),
(evo ga!),  ,
,  ,
,  . Sada dobijemo izraze slične sljedećem:
. Sada dobijemo izraze slične sljedećem: 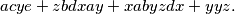 Nakon uobičajenom grupiranja (parametri na početak, varijable na kraj, hvala komutativnosti) i uvođenja potencija samo u svrhu sažetijeg zapisivanja, dobijemo sljedeći uređeni izraz:
Nakon uobičajenom grupiranja (parametri na početak, varijable na kraj, hvala komutativnosti) i uvođenja potencija samo u svrhu sažetijeg zapisivanja, dobijemo sljedeći uređeni izraz: