Nastavljamo razmatranje iz prethodnog primjera. Došli smo do polinoma 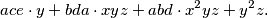 Svaki pristojan matematički objekt odaziva se na jedinstveno ime, pa bi bio red da nadjenemo jedno i našem polinomu. Neka bude:
Svaki pristojan matematički objekt odaziva se na jedinstveno ime, pa bi bio red da nadjenemo jedno i našem polinomu. Neka bude:  Od milja ćemo ga zvati skraćeno
Od milja ćemo ga zvati skraćeno  .
.
Primjetili ste da sam izbjegao znak jednakosti prilikom uvođenja imena polinoma. Zašto? Pa, Poloman je ime polinoma, što treba razlikovati od vrijednosti polinoma. Ova veličina je varijabilna, jasno, upravo zato što u polinomu imamo varijabilne parametre. Vrijednost polinoma za određeni izbor vrijednosti njegovih varijabli dobije se tako da se te određene vrijednosti varijabli uvrste u polinom i zbroje i izmnože s ostalim parametrima polinoma. Vrijednost polinoma je očito jedan broj. Njega označavamo s 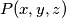 (u ovom slučaju, kad su varijable polinoma upravo
(u ovom slučaju, kad su varijable polinoma upravo  ,
,  i
i  ). Dakle, sad možemo bez straha pisati:
). Dakle, sad možemo bez straha pisati: 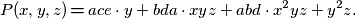
Ovo je konačno zapis koji vam izgleda poznatije. Možda jedino niste toliko navikli na polinome s više varijabli, ali cijela priča do sada nije otežana brojem varijabli u polinomu. E da, još jedna stvar, sad možemo i urediti dalje parametarski dio polinoma. Recimo, prvi djelić polinoma (monom) glasi  . No,
. No, 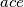 je zapravo jedan broj koji se jednostavno dobije iz vrijednosti parametara
je zapravo jedan broj koji se jednostavno dobije iz vrijednosti parametara  ,
,  i
i  . Stoga ga možemo enkapsulirati u novi parametar, recimo
. Stoga ga možemo enkapsulirati u novi parametar, recimo  (znak
(znak 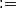 koristimo kad nešto spominjemo prvi put, tj. definiramo, i to kao jednako nečemu već poznatom). Analogno napravimo s ostalim monomima, pa dobijemo:
koristimo kad nešto spominjemo prvi put, tj. definiramo, i to kao jednako nečemu već poznatom). Analogno napravimo s ostalim monomima, pa dobijemo: 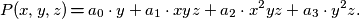
Stalno spominjem monome, ali nisam ih još definirao. Samo ime dolazi iz grčkog: mono, gr. - jedan, nome, gr. - ime. Dakle, otprilike, jedno ime, ili bolje, jedan izraz. Polinom je onda više izraza. A izraz je umnožak parametra i potencija varijabli.
Kao rješenje, upišite vrijednost parametra 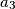 .
.
Nastavljamo razmatranje iz prethodnog primjera. Došli smo do polinoma
$$ace\cdot y + bda\cdot xyz + abd\cdot x^2yz + y^2z \text.$$
Svaki pristojan matematički objekt odaziva se na jedinstveno ime, pa bi bio red da nadjenemo jedno i našem polinomu. Neka bude:
$$ \operatorname{Poloman} \equiv ace\cdot y + bda\cdot xyz + abd\cdot x^2yz + y^2z \text.$$
Od milja ćemo ga zvati skraćeno $P$.
Primjetili ste da sam izbjegao znak jednakosti prilikom uvođenja imena polinoma. Zašto? Pa, Poloman je ime polinoma, što treba razlikovati od \emph{vrijednosti} polinoma. Ova veličina je varijabilna, jasno, upravo zato što u polinomu imamo varijabilne parametre. \emph{Vrijednost} polinoma za \underline{određeni izbor} vrijednosti njegovih varijabli dobije se tako da se te određene vrijednosti varijabli uvrste u polinom i zbroje i izmnože s ostalim parametrima polinoma. Vrijednost polinoma je očito jedan broj. Njega označavamo s $P(x, y, z)$ (u ovom slučaju, kad su varijable polinoma upravo $x$, $y$ i $z$). Dakle, sad možemo bez straha pisati:
$$ P(x, y, z)\,{\textbf{=}}\, ace\cdot y + bda\cdot xyz + abd\cdot x^2yz + y^2z \text. $$
Ovo je konačno zapis koji vam izgleda poznatije. Možda jedino niste toliko navikli na polinome s više varijabli, ali cijela priča do sada nije otežana brojem varijabli u polinomu. E da, još jedna stvar, sad možemo i urediti dalje parametarski dio polinoma. Recimo, prvi djelić polinoma (monom) glasi $ace \cdot y$. No, $ace$ je zapravo jedan broj koji se jednostavno dobije iz vrijednosti parametara $a$, $c$ i $e$. Stoga ga možemo enkapsulirati u novi parametar, recimo $a_0 := ace$ (znak $:=$ koristimo kad nešto spominjemo prvi put, tj. definiramo, i to kao jednako nečemu već poznatom). Analogno napravimo s ostalim monomima, pa dobijemo:
$$ P(x, y, z)\,{\textbf{=}}\, a_0 \cdot y + a_1 \cdot xyz + a_2 \cdot x^2yz + a_3 \cdot y^2z \text. $$
Stalno spominjem \emph{monome}, ali nisam ih još definirao. Samo ime dolazi iz grčkog: mono, gr. - jedan, nome, gr. - ime. Dakle, otprilike, jedno ime, ili bolje, jedan izraz. Polinom je onda više izraza. A izraz je umnožak parametra i potencija varijabli.
Kao rješenje, upišite vrijednost parametra $a_3$.
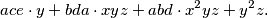 Svaki pristojan matematički objekt odaziva se na jedinstveno ime, pa bi bio red da nadjenemo jedno i našem polinomu. Neka bude:
Svaki pristojan matematički objekt odaziva se na jedinstveno ime, pa bi bio red da nadjenemo jedno i našem polinomu. Neka bude:  Od milja ćemo ga zvati skraćeno
Od milja ćemo ga zvati skraćeno  .
.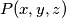 (u ovom slučaju, kad su varijable polinoma upravo
(u ovom slučaju, kad su varijable polinoma upravo  ,
,  i
i  ). Dakle, sad možemo bez straha pisati:
). Dakle, sad možemo bez straha pisati: 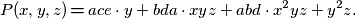
 . No,
. No, 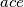 je zapravo jedan broj koji se jednostavno dobije iz vrijednosti parametara
je zapravo jedan broj koji se jednostavno dobije iz vrijednosti parametara  ,
,  i
i  . Stoga ga možemo enkapsulirati u novi parametar, recimo
. Stoga ga možemo enkapsulirati u novi parametar, recimo  (znak
(znak 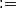 koristimo kad nešto spominjemo prvi put, tj. definiramo, i to kao jednako nečemu već poznatom). Analogno napravimo s ostalim monomima, pa dobijemo:
koristimo kad nešto spominjemo prvi put, tj. definiramo, i to kao jednako nečemu već poznatom). Analogno napravimo s ostalim monomima, pa dobijemo: 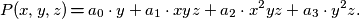
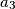 .
. 