Vrijeme: 01:56
Primjer 2: Euklidov algoritam - primjena
Koji je kardinalitet (broj članova) skupa svih cijelih brojeva  za koje je razlomak
za koje je razlomak 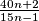 cijeli broj?
cijeli broj?
Rješenje:
Napomenimo odmah na početku rješenja kako je iz tvrdnje i dokaza Euklidovog algoritma jasno da vrijedi i 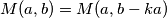 , za svaki cijeli broj
, za svaki cijeli broj  . Naime, za pozitivan
. Naime, za pozitivan  je to samo
je to samo  uzastopnih primjena (osnovnog) Euklidovog algoritma:
uzastopnih primjena (osnovnog) Euklidovog algoritma: 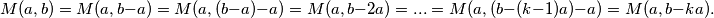
Sada raspisujemo: 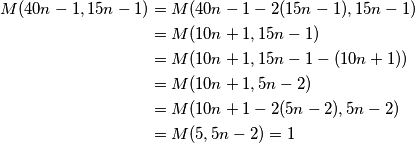
U zadnjem koraku je najveći zajednički djelitelj  jer broj
jer broj 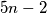 ne može biti djeljiv s
ne može biti djeljiv s  . Dakle, brojnik i nazivnik početnog razlomka su relativno prosti pa su jedini
. Dakle, brojnik i nazivnik početnog razlomka su relativno prosti pa su jedini  za koje taj razlomak može biti cijeli broj, oni za koje je vrijednost nazivnika
za koje taj razlomak može biti cijeli broj, oni za koje je vrijednost nazivnika  ili
ili  . Očito je da je jedini takav broj
. Očito je da je jedini takav broj 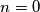 .
.
