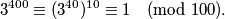Označimo s 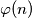 broj prirodnih brojeva manjih ili jednakih
broj prirodnih brojeva manjih ili jednakih  koji su relativno prosti s
koji su relativno prosti s  , za svaki prirodan broj
, za svaki prirodan broj  . Time smo definirali funkciju
. Time smo definirali funkciju 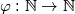 poznatu pod imenom
poznatu pod imenom 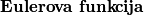 .
.
Za nju postoji i eksplicitna formula. Za  , gdje su
, gdje su  prosti, a
prosti, a 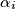 prirodni brojevi, imamo:
prirodni brojevi, imamo: 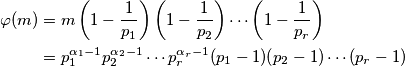
Ona ima svojstvo 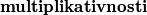 , odnosno za bilo koje relativno proste brojeve
, odnosno za bilo koje relativno proste brojeve  i
i  vrijedi
vrijedi 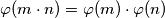
Konačno, možemo iskazati 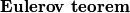 .
.
Teorem 2. Ako su  i
i  relativno prosti brojevi, onda vrijedi
relativno prosti brojevi, onda vrijedi 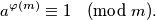
Primjer 3. Odredimo zadnju znamenku broja 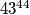 .
.
Rješenje: Budući da je od brojeva manjih od njega,  relativno prost s brojevima
relativno prost s brojevima 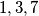 i
i  , zato je
, zato je 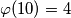 . Kako je
. Kako je 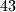 relativno prost s
relativno prost s  , vrijedi
, vrijedi 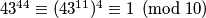 , prema Eulerovom teoremu.
, prema Eulerovom teoremu.
Primjer 4. Odredimo posljednje dvije znamenke broja 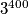 .
.
Rješenje: U ovom primjeru koristit ćemo svojstvo multiplikativnosti Eulerove funkcije te njezinu eksplicitnu formulu. Vrijedi sljedeće: 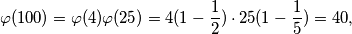 pa je
pa je 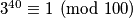 . Zato je
. Zato je 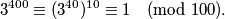
Za rješenje upišite 1.
Označimo s $\varphi(n)$ broj prirodnih brojeva manjih ili jednakih $n$ koji su relativno prosti s $n$, za svaki prirodan broj $n$. Time smo definirali funkciju $\varphi : \mathbb{N} \to \mathbb{N}$ poznatu pod imenom $\textbf{Eulerova funkcija}$.\\ \\
Za nju postoji i eksplicitna formula. Za $m=p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_r^{\alpha_r}$, gdje su $p_i$ prosti, a $\alpha_i$ prirodni brojevi, imamo:
\begin{align*}
\varphi(m)&=m\left( 1-\dfrac{1}{p_1}\right)\left( 1-\dfrac{1}{p_2}\right)\cdots \left( 1-\dfrac{1}{p_r}\right)\\
&=p_1^{\alpha_1-1}p_2^{\alpha_2-1}\cdots p_r^{\alpha_r-1}(p_1-1)(p_2-1)\cdots (p_r-1)
\end{align*} \\
Ona ima svojstvo $\textbf{multiplikativnosti}$, odnosno za bilo koje relativno proste brojeve $m$ i $n$ vrijedi $$\varphi(m\cdot n)= \varphi(m) \cdot \varphi(n)$$
Konačno, možemo iskazati $\textbf{Eulerov teorem}$. \\
\textbf{Teorem 2.} Ako su $a$ i $m$ relativno prosti brojevi, onda vrijedi $$a^{\varphi(m)}\equiv 1 \pmod{m}.$$
\textbf{Primjer 3.} Odredimo zadnju znamenku broja $43^{44}$. \\
\textbf{Rješenje:} Budući da je od brojeva manjih od njega, $10$ relativno prost s brojevima $1, 3, 7$ i $9$, zato je $\varphi(10) = 4$. Kako je $43$ relativno prost
s $10$, vrijedi $43^{44} \equiv (43^{11})^4 \equiv 1 \pmod{10}$, prema Eulerovom teoremu. \\ \\
\textbf{Primjer 4.} Odredimo posljednje dvije znamenke broja $3^{400}$. \\
\textbf{Rješenje:} U ovom primjeru koristit ćemo svojstvo multiplikativnosti Eulerove funkcije te njezinu eksplicitnu formulu. Vrijedi sljedeće:
$$ \varphi(100) = \varphi(4)\varphi(25) = 4 (1 - \frac{1}{2}) \cdot 25 (1 - \frac{1}{5}) = 40, $$
pa je $3^{40} \equiv 1 \pmod{100}$. Zato je $$ 3^{400} \equiv (3^{40})^{10} \equiv 1 \pmod{100}. $$
Za rješenje upišite 1.
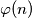 broj prirodnih brojeva manjih ili jednakih
broj prirodnih brojeva manjih ili jednakih  koji su relativno prosti s
koji su relativno prosti s  , za svaki prirodan broj
, za svaki prirodan broj  . Time smo definirali funkciju
. Time smo definirali funkciju 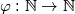 poznatu pod imenom
poznatu pod imenom 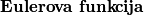 .
. , gdje su
, gdje su  prosti, a
prosti, a 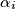 prirodni brojevi, imamo:
prirodni brojevi, imamo: 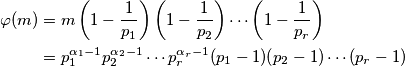
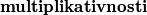 , odnosno za bilo koje relativno proste brojeve
, odnosno za bilo koje relativno proste brojeve  i
i  vrijedi
vrijedi 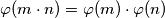
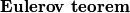 .
.  i
i  relativno prosti brojevi, onda vrijedi
relativno prosti brojevi, onda vrijedi 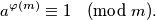
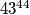 .
.  relativno prost s brojevima
relativno prost s brojevima 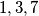 i
i  , zato je
, zato je 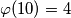 . Kako je
. Kako je 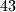 relativno prost s
relativno prost s  , vrijedi
, vrijedi 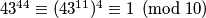 , prema Eulerovom teoremu.
, prema Eulerovom teoremu. 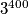 .
. 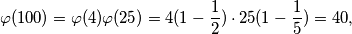 pa je
pa je 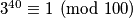 . Zato je
. Zato je