Primjer 3: Kvadratni ostatci
Definirajmo cijeli broj  kao kvadratni ostatak modulo n ako postoji cijeli broj
kao kvadratni ostatak modulo n ako postoji cijeli broj  takav da je
takav da je 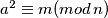 .
.
Dokažimo za neparan prosti broj  postoji točno
postoji točno 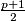 kvadratnih ostataka modulo
kvadratnih ostataka modulo  .
.
Rješenje:
Najprije primijetimo da je  očito uvijek kvadratni ostatak jer je, primjerice,
očito uvijek kvadratni ostatak jer je, primjerice, 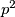 uvijek djeljiv s
uvijek djeljiv s  .
.
Neka je sada 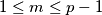 . Primijetimo da je
. Primijetimo da je 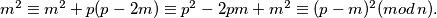 Dakle, kvadrati od
Dakle, kvadrati od  i
i 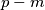 daju jednake ostatke modulo
daju jednake ostatke modulo  , za svaki promatrani
, za svaki promatrani  , što znači da možemo imati maksimalno
, što znači da možemo imati maksimalno 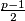 kvadratnih ostataka u skupu
kvadratnih ostataka u skupu 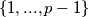 .
.
S druge strane, pretpostavimo da su 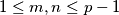 takvi da je
takvi da je 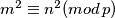 . U tom je slučaju
. U tom je slučaju 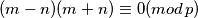 , tj neki od brojeva
, tj neki od brojeva  i
i  je djeljiv s
je djeljiv s  . To onda implicira da vrijedi ili
. To onda implicira da vrijedi ili 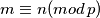 ili
ili 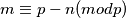 . Dakle, svaki od
. Dakle, svaki od 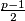 parova ostataka
parova ostataka 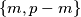 iz skupa
iz skupa 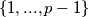 daje različite kvadratne ostatke module
daje različite kvadratne ostatke module  pa ih zaista ima točno
pa ih zaista ima točno 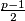 .
.
Kao rješenje primjera, navedite koliko kvadratnih ostataka ima jedini prosti broj kojeg nismo pokrili ovim teoremom.
