MetaMath '22

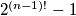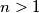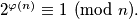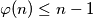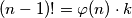\textbf{Primjer 5.} Pokažite ako je $n$ neparni cijeli broj, onda $n$ dijeli $2^{(n-1)!} - 1$. \\ \textbf{Rješenje:} Tvrdnja je očita za $n=1$, pa pretpostavimo $n>1$. Po Eulerovom teoremu $2^{\varphi(n)} \equiv 1 \pmod n.$ Kako je $\varphi(n) \leq n-1$ imamo $(n-1)! = \varphi(n) \cdot k$, za neki cijeli broj $k$. Dakle, $$ 2^{(n-1)!} \equiv 2^{\varphi(n) \cdot k} \equiv \left(2^{\varphi(n)}\right)^k \equiv 1^k \equiv 1 \pmod n. 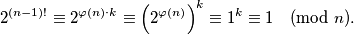$$ VIše primjera o Malom Fermatovom i Eulerovom teoremu možete pogledati na: \href{https://mnm.hr/wp-content/uploads/2015/10/mali_fermat_i_euler.pdf}{MNM Online predavanje: MFT i Euler}. Za rješenje upišite 1.