Vrijeme: 01:52
Primjer 1.: Mali Fermatov teorem
U ovom predavanju proći ćemo jedan od osnovnih teorema u teoriji brojeva; Mali Fermatov teorem te njegovo poopćenje Eulerov teorem.
Teorem 1.  Neka je
Neka je  cijeli broj i
cijeli broj i  prost broj koji ne dijeli
prost broj koji ne dijeli  . Tada vrijedi:
. Tada vrijedi: 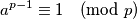
Kako su  i
i  relativno prosti vrijedi:
relativno prosti vrijedi: 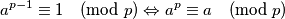
Također, ukoliko 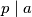 , onda imamo
, onda imamo 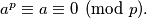 Zato tvrdnju malog Fermatovog teorema možemo i ovako izreći:
Zato tvrdnju malog Fermatovog teorema možemo i ovako izreći:
Za svaki prost broj  i svaki prirodan broj
i svaki prirodan broj  vrijedi:
vrijedi: 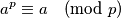
Dokaz MFT-a možete pogledati ovdje.
Primjer 1. Ako su  i
i  različiti prosti brojevi, dokažite da je broj
različiti prosti brojevi, dokažite da je broj 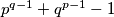 djeljiv sa
djeljiv sa 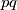 .
.
Rješenje: Po malom Fermatovom teoremu imamo 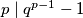 ,
, 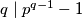 , a odavde slijedi
, a odavde slijedi 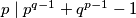 ,
, 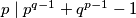 . Budući da su
. Budući da su  i
i  relativno prosti, slijedi tvrdnja zadatka.
relativno prosti, slijedi tvrdnja zadatka.
Za rješenje upišite 1.
