Riješite jednadžbu 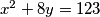 u cijelim brojevima.
u cijelim brojevima.
Rješenje:
Ideja koju ćemo primijeniti ovdje često se koristi u ovakvim zadacima. Cilj je promotriti jednadžbu modulo  , za neki
, za neki  za kojeg ćemo moći eliminirati što više potencijalnih rješenja i svesti zadatak na jednostavniji problem. Primjerice, ovdje ćemo promotriti jednadžbu modulo
za kojeg ćemo moći eliminirati što više potencijalnih rješenja i svesti zadatak na jednostavniji problem. Primjerice, ovdje ćemo promotriti jednadžbu modulo  , zato što time "nestaje" član
, zato što time "nestaje" član 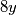 iz jednadžbe, budući da je taj izraz djeljiv s
iz jednadžbe, budući da je taj izraz djeljiv s  neovisno o vrijednosti
neovisno o vrijednosti  . Dakle, svako potencijano rješenje promatrane jednadžbe mora zadovoljavati:
. Dakle, svako potencijano rješenje promatrane jednadžbe mora zadovoljavati: 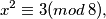 jer je
jer je 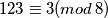 . Sada možemo samo uvrstiti sve moguće ostatke modulo
. Sada možemo samo uvrstiti sve moguće ostatke modulo  umjesto
umjesto  i provjeriti daje li ijedan od njih nakon kvadriranja ostatak
i provjeriti daje li ijedan od njih nakon kvadriranja ostatak  pri dijeljenju s
pri dijeljenju s  .
.
Ipak, možemo i nešto pametnije pristupiti problemu i dodatno olakšati posao. Primijetimo da je kvadrat svakog parnog broja nužno djeljiv sa  . No, ako je broj djeljiv s
. No, ako je broj djeljiv s  , jedini ostatci koje on može davati pri dijeljenju s
, jedini ostatci koje on može davati pri dijeljenju s  su
su  i
i  . Dakle,
. Dakle,  svakako ne može biti paran broj.
svakako ne može biti paran broj.
Nadalje, ako se sjetimo primjera 3, ondje smo komentirali da kvadrati od  i
i  uvijek daju jednake ostatke pri dijeljenju s
uvijek daju jednake ostatke pri dijeljenju s  . Koristeći tu opservaciju, uz prethodnu koja nam govori da je
. Koristeći tu opservaciju, uz prethodnu koja nam govori da je  nužno neparan, preostaje nam samo provjeriti kakve ostatke modulo
nužno neparan, preostaje nam samo provjeriti kakve ostatke modulo  daju
daju 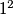 i
i 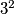 . Odgovor je u oba slučaja očito
. Odgovor je u oba slučaja očito  , pa možemo zaključiti da ne postoji cijeli broj
, pa možemo zaključiti da ne postoji cijeli broj  čiji kvadrat daje ostatak
čiji kvadrat daje ostatak  pri dijeljenju s
pri dijeljenju s  , a samim time ne postoji niti jedno rješenje početne jednadžbe.
, a samim time ne postoji niti jedno rješenje početne jednadžbe.
Možda se ove napomene čine nepotrebne s obzirom da nije tako teško izračunati kvadrate  brojeva modulo
brojeva modulo  , ali u praksi možemo imati puno veći broj potrebnih uvrštavanja i zato tu kompleksnost uvijek pokušavamo reducirati "pametnim" trikovima i opservacijama poput ovih ovdje.
, ali u praksi možemo imati puno veći broj potrebnih uvrštavanja i zato tu kompleksnost uvijek pokušavamo reducirati "pametnim" trikovima i opservacijama poput ovih ovdje.
Sada ste spremni za napadanje ovotjednih zadataka. Kao rješenje upišite  i sretno dalje! :)
i sretno dalje! :)
Riješite jednadžbu $x^2 + 8y = 123$ u cijelim brojevima.
\textbf{Rješenje:}
Ideja koju ćemo primijeniti ovdje često se koristi u ovakvim zadacima. Cilj je promotriti jednadžbu modulo $n$, za neki $n$ za kojeg ćemo moći eliminirati što više potencijalnih rješenja i svesti zadatak na jednostavniji problem. Primjerice, ovdje ćemo promotriti jednadžbu modulo $8$, zato što time "nestaje" član $8y$ iz jednadžbe, budući da je taj izraz djeljiv s $8$ neovisno o vrijednosti $y$. Dakle, svako potencijano rješenje promatrane jednadžbe mora zadovoljavati:
$$x^2 \equiv 3 (mod \, 8),$$
jer je $123 \equiv 3 (mod \, 8)$. Sada možemo samo uvrstiti sve moguće ostatke modulo $8$ umjesto $x$ i provjeriti daje li ijedan od njih nakon kvadriranja ostatak $3$ pri dijeljenju s $8$.
Ipak, možemo i nešto pametnije pristupiti problemu i dodatno olakšati posao. Primijetimo da je kvadrat svakog parnog broja nužno djeljiv sa $4$. No, ako je broj djeljiv s $4$, jedini ostatci koje on može davati pri dijeljenju s $8$ su $0$ i $4$. Dakle, $x$ svakako ne može biti paran broj.
Nadalje, ako se sjetimo \textbf{primjera 3}, ondje smo komentirali da kvadrati od $x$ i $n-x$ uvijek daju jednake ostatke pri dijeljenju s $n$. Koristeći tu opservaciju, uz prethodnu koja nam govori da je $x$ nužno neparan, preostaje nam samo provjeriti kakve ostatke modulo $8$ daju $1^2$ i $3^2$. Odgovor je u oba slučaja očito $1$, pa možemo zaključiti da ne postoji cijeli broj $x$ čiji kvadrat daje ostatak $3$ pri dijeljenju s $8$, a samim time ne postoji niti jedno rješenje početne jednadžbe.
Možda se ove napomene čine nepotrebne s obzirom da nije tako teško izračunati kvadrate $8$ brojeva modulo $8$, ali u praksi možemo imati puno veći broj potrebnih uvrštavanja i zato tu kompleksnost uvijek pokušavamo reducirati "pametnim" trikovima i opservacijama poput ovih ovdje.
Sada ste spremni za napadanje ovotjednih zadataka. Kao rješenje upišite $0$ i sretno dalje! :)
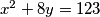 u cijelim brojevima.
u cijelim brojevima. , za neki
, za neki  za kojeg ćemo moći eliminirati što više potencijalnih rješenja i svesti zadatak na jednostavniji problem. Primjerice, ovdje ćemo promotriti jednadžbu modulo
za kojeg ćemo moći eliminirati što više potencijalnih rješenja i svesti zadatak na jednostavniji problem. Primjerice, ovdje ćemo promotriti jednadžbu modulo  , zato što time "nestaje" član
, zato što time "nestaje" član 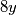 iz jednadžbe, budući da je taj izraz djeljiv s
iz jednadžbe, budući da je taj izraz djeljiv s  neovisno o vrijednosti
neovisno o vrijednosti  . Dakle, svako potencijano rješenje promatrane jednadžbe mora zadovoljavati:
. Dakle, svako potencijano rješenje promatrane jednadžbe mora zadovoljavati: 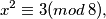 jer je
jer je 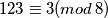 . Sada možemo samo uvrstiti sve moguće ostatke modulo
. Sada možemo samo uvrstiti sve moguće ostatke modulo  umjesto
umjesto  i provjeriti daje li ijedan od njih nakon kvadriranja ostatak
i provjeriti daje li ijedan od njih nakon kvadriranja ostatak  pri dijeljenju s
pri dijeljenju s  .
. . No, ako je broj djeljiv s
. No, ako je broj djeljiv s  , jedini ostatci koje on može davati pri dijeljenju s
, jedini ostatci koje on može davati pri dijeljenju s  su
su  i
i  . Dakle,
. Dakle,  svakako ne može biti paran broj.
svakako ne može biti paran broj. i
i  uvijek daju jednake ostatke pri dijeljenju s
uvijek daju jednake ostatke pri dijeljenju s  . Koristeći tu opservaciju, uz prethodnu koja nam govori da je
. Koristeći tu opservaciju, uz prethodnu koja nam govori da je  nužno neparan, preostaje nam samo provjeriti kakve ostatke modulo
nužno neparan, preostaje nam samo provjeriti kakve ostatke modulo  daju
daju 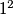 i
i 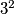 . Odgovor je u oba slučaja očito
. Odgovor je u oba slučaja očito  , pa možemo zaključiti da ne postoji cijeli broj
, pa možemo zaključiti da ne postoji cijeli broj  čiji kvadrat daje ostatak
čiji kvadrat daje ostatak  pri dijeljenju s
pri dijeljenju s  , a samim time ne postoji niti jedno rješenje početne jednadžbe.
, a samim time ne postoji niti jedno rješenje početne jednadžbe. brojeva modulo
brojeva modulo  , ali u praksi možemo imati puno veći broj potrebnih uvrštavanja i zato tu kompleksnost uvijek pokušavamo reducirati "pametnim" trikovima i opservacijama poput ovih ovdje.
, ali u praksi možemo imati puno veći broj potrebnih uvrštavanja i zato tu kompleksnost uvijek pokušavamo reducirati "pametnim" trikovima i opservacijama poput ovih ovdje. i sretno dalje! :)
i sretno dalje! :) 