Vrijeme: 02:04

Upisana i pripisana kružnica - Lanac 0 - Zadatak 4

Došlo je vrijeme da definiramo pripisanu kružnicu: A-pripisana kružnica trokuta je ona kojoj su pravci na kojima leže stranice trokuta tangente, a jedina stranica trokuta koju dira je ona nasuprot vrha A.

Njezino središte je sjecište simetrala kuta trokuta u vrhu A i vanjskih kuteva u B i C.

Pripisane kružnice imaju mnoga lijepa svojstva u odnosu na upisanu kružnicu, a vaš će zadatak biti dokazati sljedeća svojstva: 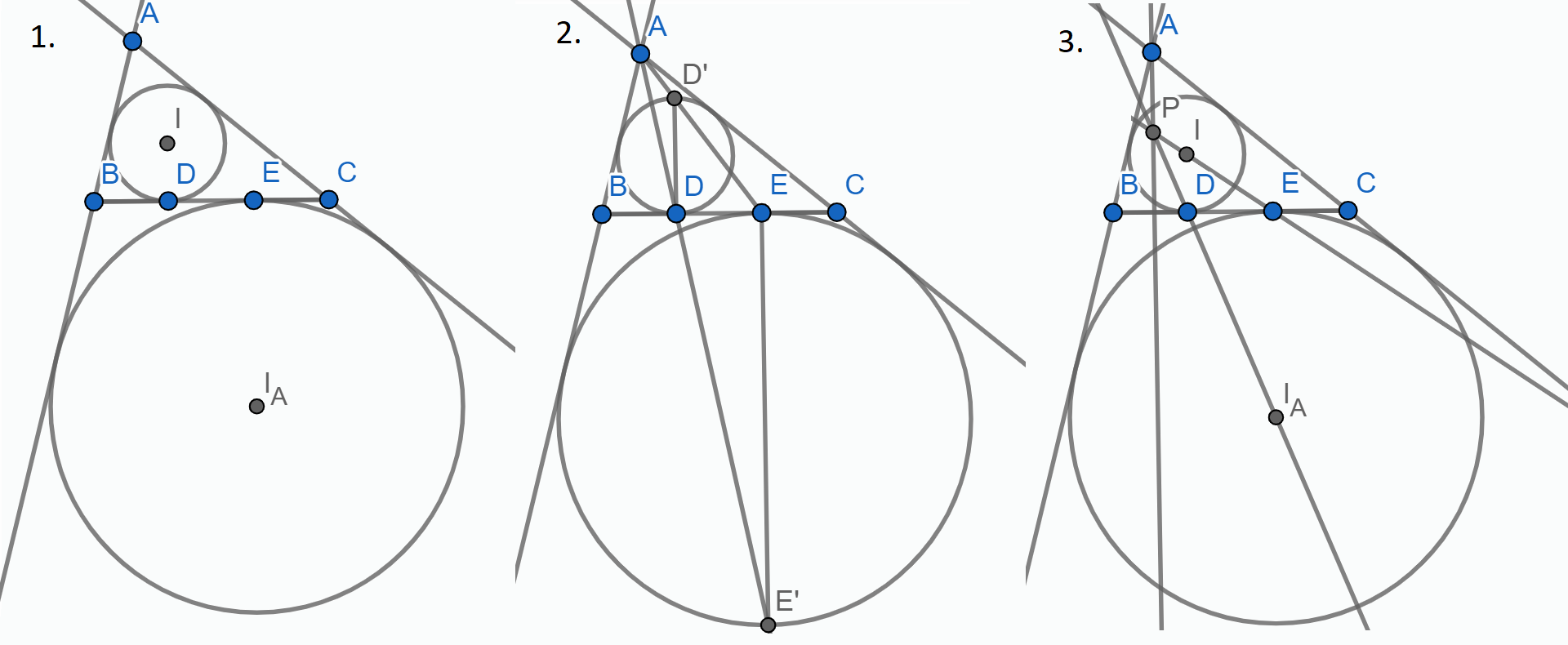\begin{enumerate} \item Vrijedi $BD = CE$. \item Spojnica $A$ i dirališta pripisane kružnice $E$ siječe upisanu kružnicu u točki dijametralno suprotnoj diralištu upisane $D$. Drugim riječima, $A$ $D'$ i $E$ su kolinearne, gdje je $D'$ točka dijametralno suprotna točki $D$. Na sličan način, $A$, $D$ i $E'$ su kolinearne, gdje je $E'$ točka dijametralno suprotna točki $E$ \item Pravci $IE$ i $I_AD$ sijeku se u polovištu visine iz $A$. \end{enumerate} Attachment Lm41.png Napomena: Ove činjenice malo se elegantnije dokažu primjenom homotetije.