Na natjecanjima se često pojavljuju zadaci s upisanim kružnicama u kojima znamo nešto o odnosu stranica.
Zadatak: Ako je zbroj duljina dviju stranica raznostraničnog trokuta jednak dvostrukoj duljini treće stranice, dokaži da je pravac kroz središte upisane kružnice i težište trokuta paralelan sa stranicom koja je srednja po duljini.
Rješenje:
Prisjetimo se formule za površinu trokuta preko radijusa upisane kružnice - uvjet 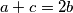 bi je mogao znatno pojednostaviti:
bi je mogao znatno pojednostaviti: 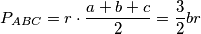 Prikažemo li sada površinu trokuta
Prikažemo li sada površinu trokuta  preko stranice
preko stranice  i odgovarajuće visine, imamo
i odgovarajuće visine, imamo 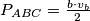 , iz čega lako dobijemo
, iz čega lako dobijemo 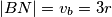 .
.
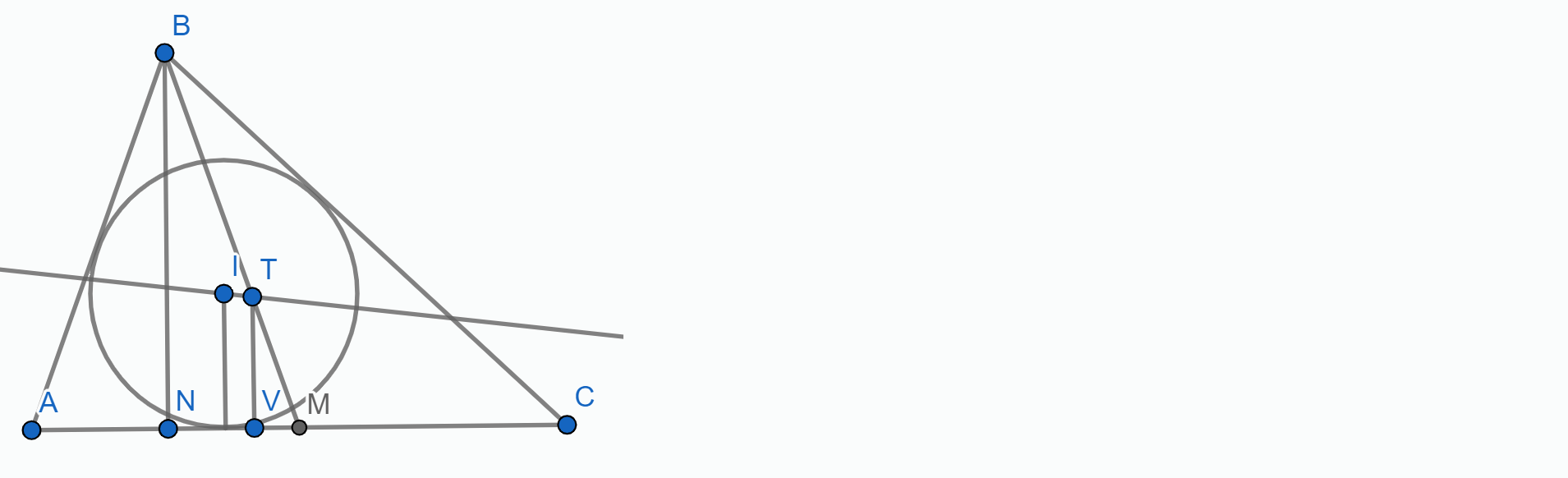
Povucimo visinu na  iz
iz  i označimo njeno nožište s
i označimo njeno nožište s  . Kada bismo dokazali da je
. Kada bismo dokazali da je 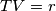 , bili bismo gotovi jer bi i
, bili bismo gotovi jer bi i  i
i  bili jednako udaljeni od pravca
bili jednako udaljeni od pravca  , a kako su mu s iste strane to bi značilo da je
, a kako su mu s iste strane to bi značilo da je 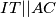 .
.
Primijetimo sada da su trokuti 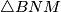 i
i 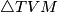 slični po
slični po  poučku jer im je šiljasti kut u vrhu
poučku jer im je šiljasti kut u vrhu  zajednički, a oba su pravokutna. Zato
zajednički, a oba su pravokutna. Zato 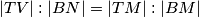 . Sjetimo li se svojstava težišta, shvatit ćemo da znamo da je omjer u kojem ono dijeli težišnicu
. Sjetimo li se svojstava težišta, shvatit ćemo da znamo da je omjer u kojem ono dijeli težišnicu  naprama
naprama  od vrha prema stranici, stoga je
od vrha prema stranici, stoga je 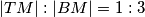 .
.
Dakle, 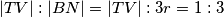 iz čega zaključujemo da je
iz čega zaključujemo da je 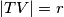 , stoga smo gotovi.
, stoga smo gotovi.
Kao rješenje upišite najmanji prosti broj djeljiv s 2.
Na natjecanjima se često pojavljuju zadaci s upisanim kružnicama u kojima znamo nešto o odnosu stranica.
\textbf{Zadatak:} Ako je zbroj duljina dviju stranica raznostraničnog trokuta jednak dvostrukoj duljini treće stranice, dokaži da je pravac kroz središte upisane kružnice i težište trokuta paralelan sa stranicom koja je srednja po duljini.
\textbf{Rješenje: }
Prisjetimo se formule za površinu trokuta preko radijusa upisane kružnice - uvjet $a+c = 2b$ bi je mogao znatno pojednostaviti:
$$P_{ABC} = r\cdot \frac{a+b+c}{2} = \frac 32 br$$
Prikažemo li sada površinu trokuta $\triangle ABC$ preko stranice $AC$ i odgovarajuće visine, imamo $P_{ABC} = \frac{b\cdot v_b}{2}$, iz čega lako dobijemo $|BN| = v_b = 3r$.
\includegraphics{stuff.png}
Povucimo visinu na $AC$ iz $T$ i označimo njeno nožište s $V$. Kada bismo dokazali da je $TV=r$, bili bismo gotovi jer bi i $I$ i $T$ bili jednako udaljeni od pravca $AC$, a kako su mu s iste strane to bi značilo da je $IT || AC$. \\
Primijetimo sada da su trokuti $\triangle BNM$ i $\triangle TVM$ slični po $K-K$ poučku jer im je šiljasti kut u vrhu $M$ zajednički, a oba su pravokutna. Zato $|TV|:|BN|= |TM|:|BM|$. Sjetimo li se \href{https://mnm.hr/wp-content/uploads/2015/10/karakteristicne_tocke_trokuta.pdf}{svojstava težišta}, shvatit ćemo da znamo da je omjer u kojem ono dijeli težišnicu $2$ naprama $1$ od vrha prema stranici, stoga je $|TM|:|BM| = 1:3$.
Dakle,
$$|TV| : |BN| = |TV| : 3r = 1 : 3$$
iz čega zaključujemo da je $|TV| = r$, stoga smo gotovi.
Kao rješenje upišite najmanji prosti broj djeljiv s 2.
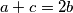 bi je mogao znatno pojednostaviti:
bi je mogao znatno pojednostaviti: 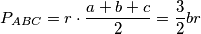 Prikažemo li sada površinu trokuta
Prikažemo li sada površinu trokuta  preko stranice
preko stranice  i odgovarajuće visine, imamo
i odgovarajuće visine, imamo 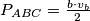 , iz čega lako dobijemo
, iz čega lako dobijemo 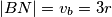 .
.
 iz
iz  i označimo njeno nožište s
i označimo njeno nožište s  . Kada bismo dokazali da je
. Kada bismo dokazali da je 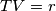 , bili bismo gotovi jer bi i
, bili bismo gotovi jer bi i  i
i  bili jednako udaljeni od pravca
bili jednako udaljeni od pravca  , a kako su mu s iste strane to bi značilo da je
, a kako su mu s iste strane to bi značilo da je 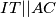 .
. 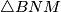 i
i 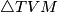 slični po
slični po  poučku jer im je šiljasti kut u vrhu
poučku jer im je šiljasti kut u vrhu  zajednički, a oba su pravokutna. Zato
zajednički, a oba su pravokutna. Zato 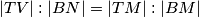 . Sjetimo li se svojstava težišta, shvatit ćemo da znamo da je omjer u kojem ono dijeli težišnicu
. Sjetimo li se svojstava težišta, shvatit ćemo da znamo da je omjer u kojem ono dijeli težišnicu  naprama
naprama  od vrha prema stranici, stoga je
od vrha prema stranici, stoga je 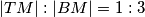 .
.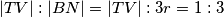 iz čega zaključujemo da je
iz čega zaključujemo da je 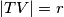 , stoga smo gotovi.
, stoga smo gotovi.