Za kraj ćemo baciti oko na rješenje jednog zadatka s upisanom kružnicom koji se pojavio na državnom natjecanju. Kroz rješenje ćemo proći neformalno, s naglaskom na proces rješavanja - kako bismo do ovako nečega mogli doći na natjecanju. Detaljno rješenje možete proučiti na linku.
Zadatak: Upisana kružnica dodiruje stranice  i
i  trokuta
trokuta  u točkama
u točkama  i
i  . Neka je
. Neka je  sjecište pravca
sjecište pravca  i simetrale kuta
i simetrale kuta 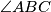 . Dokaži da je
. Dokaži da je 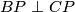 .
.
Rješenje:
1. korak Odlučujem da želim dokazati da je 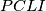 tetivan
tetivan
Za početak, bilo bi prirodno uvesti oznaku za središte upisane kružnice  i diralište upisane kružnice sa stranicom
i diralište upisane kružnice sa stranicom  ,
,  . Kako bismo mogli dokazati da je traženi kut pravi? Najbezbolniji put bi mogao biti tražiti neki tetivni četverokut. Imam li kandidata? Da - kad bismo dokazali da je četverokut
. Kako bismo mogli dokazati da je traženi kut pravi? Najbezbolniji put bi mogao biti tražiti neki tetivni četverokut. Imam li kandidata? Da - kad bismo dokazali da je četverokut 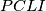 tetivan, bili bismo gotovi! Je li to četverokut kojem je razumno računati kuteve? Da, ne djeluje preteško, kut
tetivan, bili bismo gotovi! Je li to četverokut kojem je razumno računati kuteve? Da, ne djeluje preteško, kut 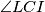 već imam zbog upisane kružnice... Da, ima smisla probati! Još neki kandidat? Ako imam nespretno nacrtanu skicu mogla bih se zeznuti na natjecanju pa gledati
već imam zbog upisane kružnice... Da, ima smisla probati! Još neki kandidat? Ako imam nespretno nacrtanu skicu mogla bih se zeznuti na natjecanju pa gledati 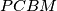 , ali naravno, kut
, ali naravno, kut 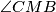 nije pravi jer
nije pravi jer 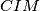 nisu kolinearne.
nisu kolinearne. 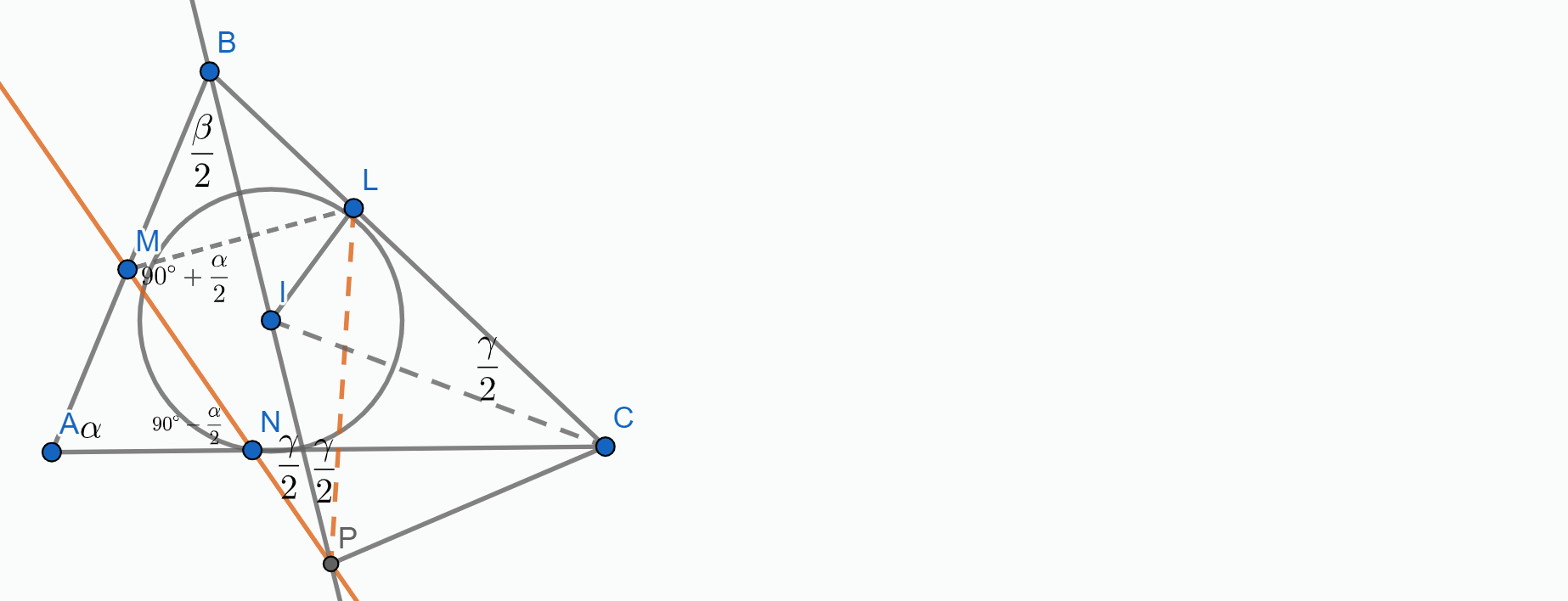
2. korak Računam kut 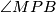
Sad kad sam odlučila što radim, označim na skici sve kuteve koji mi djeluju korisno, a mogu ih izračunati. Zato sam označila 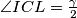 . Mogu li nekako dobiti kut
. Mogu li nekako dobiti kut 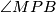 ? Pa mogu! Kut
? Pa mogu! Kut 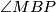 je
je 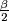 , a kut
, a kut  je vanjski kut trokuta
je vanjski kut trokuta 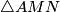 . Sad se sjetim svojstava upisane kružnice - vrijedi
. Sad se sjetim svojstava upisane kružnice - vrijedi 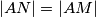 . Dakle,
. Dakle, 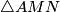 je jednakokračan, stoga je
je jednakokračan, stoga je 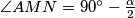 . Sada slijedi da je
. Sada slijedi da je 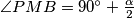 , stoga je
, stoga je 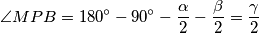
3. korak Uočavam deltoid
Hmm, računala sam  kuta i oba su ispala
kuta i oba su ispala 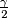 ... Da sam ih barem dobila na boljim mjestima, mogla bih odmah završiti zadatak... Konkretno, da sam dobila
... Da sam ih barem dobila na boljim mjestima, mogla bih odmah završiti zadatak... Konkretno, da sam dobila 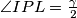 , bila bih gotova. Kutevi
, bila bih gotova. Kutevi  i ovaj kut
i ovaj kut 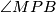 , odnosno
, odnosno  su jako slični, skoro da je jedan zrcalna slika drugog. Malo se bolje zagledam i vidim da to stvarno je tako! Naime, trokut
su jako slični, skoro da je jedan zrcalna slika drugog. Malo se bolje zagledam i vidim da to stvarno je tako! Naime, trokut 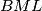 je jednakokračan jer su
je jednakokračan jer su  i
i  dirališta upisane kružnice, a
dirališta upisane kružnice, a 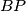 je onda, kao simetrala kuta nasuprot osnovice jednakokračnog trokuta, ujedno i visina na
je onda, kao simetrala kuta nasuprot osnovice jednakokračnog trokuta, ujedno i visina na 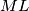 . To znači da je na nju okomita te da ju (jer je trokut jednakokračan) raspolavlja. Opće je poznato da je četverokut čije su dijagonale okomite i jedna dijagonala raspolavlja drugu deltoid! Sada mogu zaključiti da je
. To znači da je na nju okomita te da ju (jer je trokut jednakokračan) raspolavlja. Opće je poznato da je četverokut čije su dijagonale okomite i jedna dijagonala raspolavlja drugu deltoid! Sada mogu zaključiti da je  . Napomena: mogli smo samo uočiti sukladnost trokuta
. Napomena: mogli smo samo uočiti sukladnost trokuta 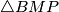 i
i 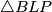 bez spominjanja svojstava deltoida.
bez spominjanja svojstava deltoida.
4. korak Jej!
Primijetimo da sada imamo 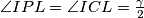 , stoga je četverokut
, stoga je četverokut 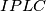 tetivan, pa je
tetivan, pa je 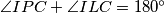 , a kako je
, a kako je 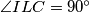 , možemo zaključiti da je
, možemo zaključiti da je 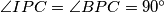 , pa je
, pa je 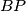 okomito na
okomito na 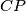 , što je trebalo dokazati.
, što je trebalo dokazati.
Super, riješili smo zadatak! U ovom zadatku vidjeli smo kako označavanje nekoliko točaka za koje je prirodno da su na skici može bitno olakšati zadatak. Kao rješenje upišite najveći prosti broj djeljiv i s 1 i s 2.
Za kraj ćemo baciti oko na rješenje jednog zadatka s upisanom kružnicom koji se pojavio na državnom natjecanju. Kroz rješenje ćemo proći neformalno, s naglaskom na proces rješavanja - kako bismo do ovako nečega mogli doći na natjecanju. Detaljno rješenje možete proučiti na \href{http://www.antonija-horvatek.from.hr/natjecanja-iz-matematike/zadaci/2010/2010-SS-drz-1234-AB-zad%2Brj/2010-SS-drz-1234-A-rj.pdf}{linku}.
\textbf{Zadatak:} Upisana kružnica dodiruje stranice $\overline{AB}$ i $\overline{AC}$ trokuta $ABC$ u točkama $M$ i $N$. Neka je $P$ sjecište pravca $MN$ i simetrale kuta $\angle{ABC}$. Dokaži da je $BP \perp CP$.
\textbf{Rješenje:}
\\
\textbf{1. korak} Odlučujem da želim dokazati da je $PCLI$ tetivan \\
Za početak, bilo bi prirodno uvesti oznaku za središte upisane kružnice $I$ i diralište upisane kružnice sa stranicom $\overline BC$, $L$.
Kako bismo mogli dokazati da je traženi kut pravi? Najbezbolniji put bi mogao biti tražiti neki tetivni četverokut. Imam li kandidata? Da - kad bismo dokazali da je četverokut $PCLI$ tetivan, bili bismo gotovi! Je li to četverokut kojem je razumno računati kuteve? Da, ne djeluje preteško, kut $\angle LCI$ već imam zbog upisane kružnice... Da, ima smisla probati!
Još neki kandidat? Ako imam nespretno nacrtanu skicu mogla bih se zeznuti na natjecanju pa gledati $PCBM$, ali naravno, kut $\angle CMB$ \textbf{nije pravi} jer $CIM$ nisu kolinearne.
\includegraphics{skizza.png}
\textbf{2. korak} Računam kut $\angle MPB$ \\
Sad kad sam odlučila što radim, označim na skici sve kuteve koji mi djeluju korisno, a mogu ih izračunati. Zato sam označila $\angle ICL = \frac\gamma2$. Mogu li nekako dobiti kut $\angle MPB$? Pa mogu! Kut $\angle MBP$ je $\frac\beta2$, a kut $\angle PMB$ je vanjski kut trokuta $\triangle AMN$. Sad se sjetim svojstava upisane kružnice - vrijedi $|AN| = |AM|$. Dakle, $\triangle AMN$ je jednakokračan, stoga je $\angle AMN = 90^\circ-\frac\alpha2$. Sada slijedi da je $\angle PMB = 90^\circ + \frac\alpha2$, stoga je
$$\angle MPB = 180^\circ - 90^\circ -\frac\alpha2-\frac\beta2 =\frac\gamma2$$
\textbf{3. korak} Uočavam deltoid \\
Hmm, računala sam $2$ kuta i oba su ispala $\frac\gamma2$... Da sam ih barem dobila na boljim mjestima, mogla bih odmah završiti zadatak... Konkretno, da sam dobila $\angle IPL = \frac\gamma2$, bila bih gotova. Kutevi $\angle IPL$ i ovaj kut $\angle MPB$, odnosno $\angle MPI$ su jako slični, skoro da je jedan zrcalna slika drugog. Malo se bolje zagledam i vidim da to stvarno je tako! Naime, trokut $BML$ je jednakokračan jer su $M$ i $L$ dirališta upisane kružnice, a $BP$ je onda, kao simetrala kuta nasuprot osnovice jednakokračnog trokuta, ujedno i visina na $ML$. To znači da je na nju okomita te da ju (jer je trokut jednakokračan) raspolavlja. Opće je poznato da je četverokut čije su dijagonale okomite i jedna dijagonala raspolavlja drugu deltoid! Sada mogu zaključiti da je $\angle IPL = \angle MPI = \angle \frac\gamma2$.
Napomena: mogli smo samo uočiti sukladnost trokuta $\triangle BMP$ i $\triangle BLP$ bez spominjanja svojstava deltoida.
\textbf{4. korak} Jej! \\
Primijetimo da sada imamo $\angle IPL = \angle ICL = \frac\gamma 2$, stoga je četverokut $IPLC$ tetivan, pa je $\angle IPC + \angle ILC = 180^\circ$, a kako je $\angle ILC = 90^\circ$, možemo zaključiti da je $\angle IPC = \angle BPC = 90^\circ$, pa je $BP$ okomito na $CP$, što je trebalo dokazati.
Super, riješili smo zadatak! U ovom zadatku vidjeli smo kako označavanje nekoliko točaka za koje je prirodno da su na skici može bitno olakšati zadatak.
Kao rješenje upišite najveći prosti broj djeljiv i s 1 i s 2.
 i
i  trokuta
trokuta  u točkama
u točkama  i
i  . Neka je
. Neka je  sjecište pravca
sjecište pravca  i simetrale kuta
i simetrale kuta 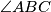 . Dokaži da je
. Dokaži da je 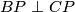 .
.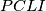 tetivan
tetivan  i diralište upisane kružnice sa stranicom
i diralište upisane kružnice sa stranicom  ,
,  . Kako bismo mogli dokazati da je traženi kut pravi? Najbezbolniji put bi mogao biti tražiti neki tetivni četverokut. Imam li kandidata? Da - kad bismo dokazali da je četverokut
. Kako bismo mogli dokazati da je traženi kut pravi? Najbezbolniji put bi mogao biti tražiti neki tetivni četverokut. Imam li kandidata? Da - kad bismo dokazali da je četverokut 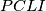 tetivan, bili bismo gotovi! Je li to četverokut kojem je razumno računati kuteve? Da, ne djeluje preteško, kut
tetivan, bili bismo gotovi! Je li to četverokut kojem je razumno računati kuteve? Da, ne djeluje preteško, kut 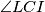 već imam zbog upisane kružnice... Da, ima smisla probati! Još neki kandidat? Ako imam nespretno nacrtanu skicu mogla bih se zeznuti na natjecanju pa gledati
već imam zbog upisane kružnice... Da, ima smisla probati! Još neki kandidat? Ako imam nespretno nacrtanu skicu mogla bih se zeznuti na natjecanju pa gledati 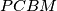 , ali naravno, kut
, ali naravno, kut 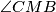 nije pravi jer
nije pravi jer 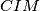 nisu kolinearne.
nisu kolinearne. 
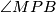
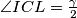 . Mogu li nekako dobiti kut
. Mogu li nekako dobiti kut 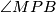 ? Pa mogu! Kut
? Pa mogu! Kut 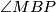 je
je 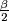 , a kut
, a kut  je vanjski kut trokuta
je vanjski kut trokuta 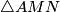 . Sad se sjetim svojstava upisane kružnice - vrijedi
. Sad se sjetim svojstava upisane kružnice - vrijedi 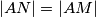 . Dakle,
. Dakle, 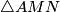 je jednakokračan, stoga je
je jednakokračan, stoga je 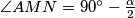 . Sada slijedi da je
. Sada slijedi da je 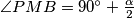 , stoga je
, stoga je 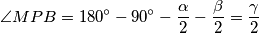
 kuta i oba su ispala
kuta i oba su ispala 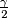 ... Da sam ih barem dobila na boljim mjestima, mogla bih odmah završiti zadatak... Konkretno, da sam dobila
... Da sam ih barem dobila na boljim mjestima, mogla bih odmah završiti zadatak... Konkretno, da sam dobila 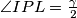 , bila bih gotova. Kutevi
, bila bih gotova. Kutevi  i ovaj kut
i ovaj kut 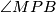 , odnosno
, odnosno  su jako slični, skoro da je jedan zrcalna slika drugog. Malo se bolje zagledam i vidim da to stvarno je tako! Naime, trokut
su jako slični, skoro da je jedan zrcalna slika drugog. Malo se bolje zagledam i vidim da to stvarno je tako! Naime, trokut 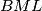 je jednakokračan jer su
je jednakokračan jer su  i
i  dirališta upisane kružnice, a
dirališta upisane kružnice, a 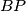 je onda, kao simetrala kuta nasuprot osnovice jednakokračnog trokuta, ujedno i visina na
je onda, kao simetrala kuta nasuprot osnovice jednakokračnog trokuta, ujedno i visina na 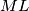 . To znači da je na nju okomita te da ju (jer je trokut jednakokračan) raspolavlja. Opće je poznato da je četverokut čije su dijagonale okomite i jedna dijagonala raspolavlja drugu deltoid! Sada mogu zaključiti da je
. To znači da je na nju okomita te da ju (jer je trokut jednakokračan) raspolavlja. Opće je poznato da je četverokut čije su dijagonale okomite i jedna dijagonala raspolavlja drugu deltoid! Sada mogu zaključiti da je  . Napomena: mogli smo samo uočiti sukladnost trokuta
. Napomena: mogli smo samo uočiti sukladnost trokuta 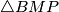 i
i 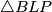 bez spominjanja svojstava deltoida.
bez spominjanja svojstava deltoida.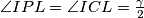 , stoga je četverokut
, stoga je četverokut 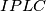 tetivan, pa je
tetivan, pa je 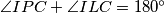 , a kako je
, a kako je 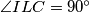 , možemo zaključiti da je
, možemo zaključiti da je 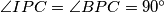 , pa je
, pa je 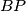 okomito na
okomito na  , što je trebalo dokazati.
, što je trebalo dokazati.