Riješit ćemo tipični primjer zadatka s upisanom kružnicom s županijske razine natjecanja. Na nižim je razinama natjecanja uobičajeno susresti zadatke koji se lako riješe metodom površine, a najbitnije je imati na umu da je središte upisane kružnice sjecište simetrala kuteva.
Zadatak: U pravokutnom trokutu  simetrale šiljastih kutova
simetrale šiljastih kutova 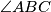 i
i 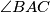 sijeku katete
sijeku katete  i
i  redom u točkama
redom u točkama  i
i  . Ako se pravci
. Ako se pravci  i
i 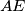 sijeku u točki
sijeku u točki  , dokažite
, dokažite 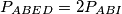
Rješenje: Ovaj je zadatak zanimljiv jer se u njemu primjenjuje i poučak o simetrali kuta koji kaže da simetrala kuta dijeli nasuprotnu stranicu u omjeru preostalih stranica. Taj nam rezultat često može pomoći u zadacima s upisanom kružnicom - ukoliko se s njim prvi put susrećete, svakako ga dokažite.
Kako je  simetrala kuta
simetrala kuta  vrijedi
vrijedi 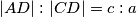 i
i 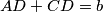 , nije teško vidjeti da
, nije teško vidjeti da 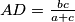 i
i 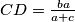 . Na isti način zaključujemo i da je
. Na isti način zaključujemo i da je 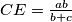 i
i 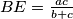 .
.
 Sada želimo izraziti površinu četverokuta
Sada želimo izraziti površinu četverokuta 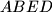 preko površine
preko površine 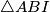 .
.
Vrijedi 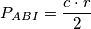 Kako je
Kako je 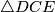 pravokutan, čini nam se zgodno izraziti
pravokutan, čini nam se zgodno izraziti 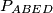 kao
kao 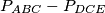 . Računamo:
. Računamo: 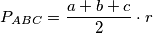
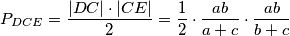 Čini nam se problematično što se u formuli za površinu
Čini nam se problematično što se u formuli za površinu 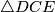 ne pojavljuje
ne pojavljuje  , ali kako je trokut
, ali kako je trokut  pravokutan, lako možemo izračunati koliki mora biti
pravokutan, lako možemo izračunati koliki mora biti  pa ga uključiti u formulu. Iz
pa ga uključiti u formulu. Iz 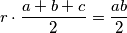 slijedi da je
slijedi da je 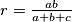 , stoga je
, stoga je 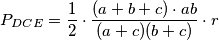
Sada jednostavno računamo
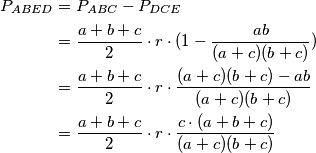
Sada prepoznamo izraz za 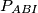 :
: 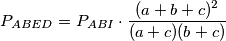
Dakle, ako dokažemo da je 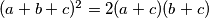 , gotovi smo. Raspisujemo:
, gotovi smo. Raspisujemo: 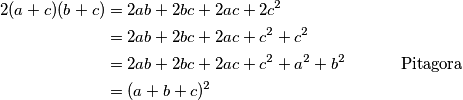
Stoga je 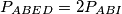 što je trebalo dokazati. Malo drugačije rješenje ovog zadatka i još puno sličnih primjera možete pronaći u MNM predavanju o metodi površine.
što je trebalo dokazati. Malo drugačije rješenje ovog zadatka i još puno sličnih primjera možete pronaći u MNM predavanju o metodi površine.
Kao rješenje upišite najmanji prosti broj djeljiv s  .
.
Riješit ćemo tipični primjer zadatka s upisanom kružnicom s županijske razine natjecanja. Na nižim je razinama natjecanja uobičajeno susresti zadatke koji se lako riješe metodom površine, a najbitnije je imati na umu da je središte upisane kružnice sjecište simetrala kuteva.
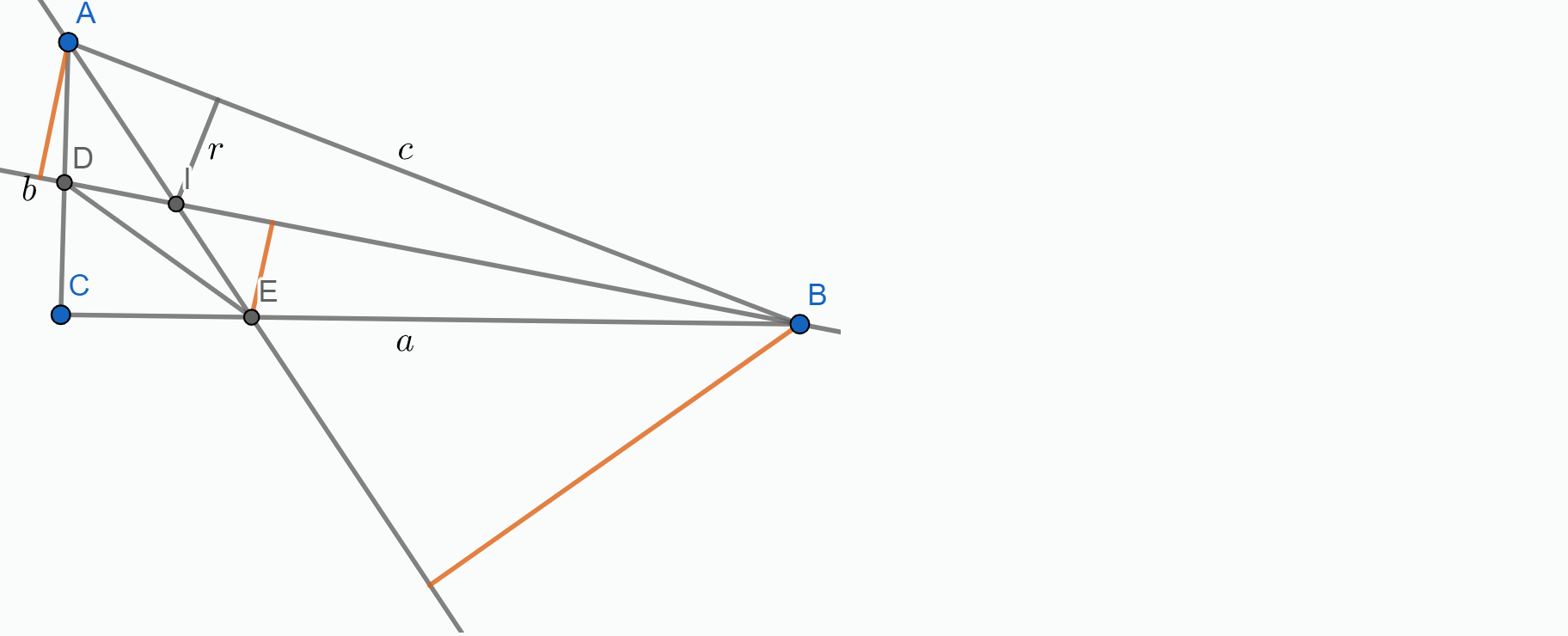
\textbf{Zadatak:} U pravokutnom trokutu $ABC$ simetrale šiljastih kutova $\angle ABC$ i $\angle BAC$ sijeku katete $AC$ i $BC$ redom u točkama
$D$ i $E$. Ako se pravci $BD$ i $AE$ sijeku u točki $I$, dokažite
$$P_{ABED} = 2P_{ABI}$$
\textbf{Rješenje:}
Ovaj je zadatak zanimljiv jer se u njemu primjenjuje i \textbf{poučak o simetrali kuta} koji kaže da simetrala kuta dijeli nasuprotnu stranicu u omjeru preostalih stranica. Taj nam rezultat često može pomoći u zadacima s upisanom kružnicom - ukoliko se s njim prvi put susrećete, svakako ga \href{https://en.wikipedia.org/wiki/Angle_bisector_theorem}{dokažite}.
\includegraphics{tmsk.png}
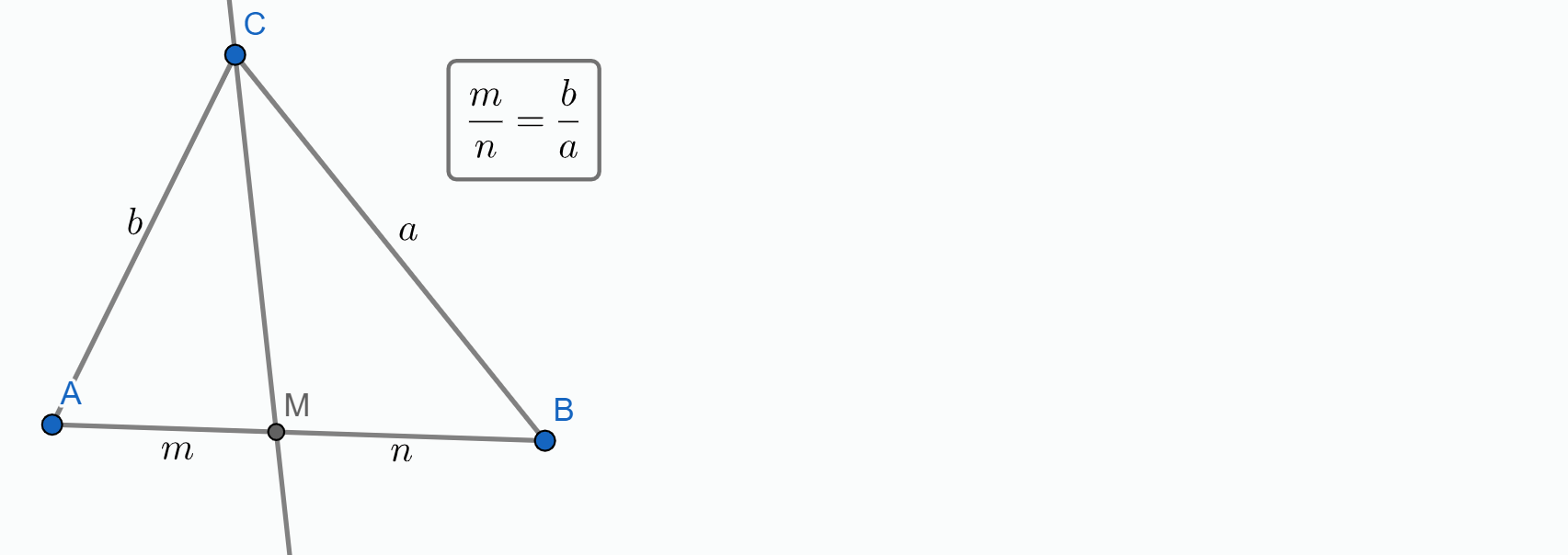
Kako je $BD$ simetrala kuta $\angle ABC$ vrijedi $|AD|:|CD| = c:a$ i $AD + CD = b$, nije teško vidjeti da $AD = \frac{bc}{a+c}$ i $CD = \frac{ba}{a+c}$. Na isti način zaključujemo i da je $CE = \frac{ab}{b+c}$ i $BE = \frac{ac}{b+c}$.
\includegraphics{pr1skica.png}
Sada želimo izraziti površinu četverokuta $ABED$ preko površine $\triangle ABI$.
Vrijedi
$$P_{ABI} = \frac{c\cdot r}{2}$$
Kako je $\triangle DCE$ pravokutan, čini nam se zgodno izraziti $P_{ABED}$ kao $P_{ABC} - P_{DCE}$. Računamo:
$$P_{ABC} = \frac{a+b+c}{2}\cdot r$$
$$P_{DCE} = \frac{|DC|\cdot |CE|}{2} = \frac{1}{2}\cdot \frac{ab}{a+c}\cdot\frac{ab}{b+c}$$
Čini nam se problematično što se u formuli za površinu $\triangle DCE$ ne pojavljuje $r$, ali kako je trokut $\triangle ABC$ pravokutan, lako možemo izračunati koliki mora biti $r$ pa ga uključiti u formulu. Iz
$$r \cdot \frac{a+b+c}{2} = \frac{ab}{2}$$
slijedi da je $r = \frac{ab}{a+b+c}$, stoga je
$$P_{DCE}=\frac{1}{2}\cdot \frac{(a+b+c)\cdot ab}{(a+c)(b+c)} \cdot r$$
Sada jednostavno računamo
$$\begin{aligned}\\
P_{ABED} &= P_{ABC} - P_{DCE} \\
&= \frac {a+b+c}2 \cdot r \cdot (1 - \frac{ab}{(a+c)(b+c)})
\\ &= \frac {a+b+c}2 \cdot r \cdot \frac{(a+c)(b+c)-ab}{(a+c)(b+c)}
\\ &= \frac{a+b+c}{2}\cdot r \cdot \frac{c\cdot (a+b+c)}{(a+c)(b+c)}
\end{aligned}$$
Sada prepoznamo izraz za $P_{ABI}$:
$$\begin{aligned}\\
P_{ABED} &= P_{ABI} \cdot \frac{ (a+b+c)^2}{(a+c)(b+c)}
\end{aligned}$$
Dakle, ako dokažemo da je $(a+b+c)^2 = 2(a+c)(b+c)$, gotovi smo. Raspisujemo:
$$\begin{aligned}\\
2(a+c)(b+c) &= 2ab + 2bc + 2ac + 2c^2\\
&= 2ab + 2bc + 2ac + c^2 + c^2
\\ &= 2ab + 2bc + 2ac + c^2 + a^2+b^2 \quad \quad \quad \text{ Pitagora}
\\ &= (a+b+c)^2
\end{aligned}$$
Stoga je
$$P_{ABED} = 2P_{ABI}$$
što je trebalo dokazati.
Malo drugačije rješenje ovog zadatka i još puno sličnih primjera možete pronaći u \href{https://mnm.hr/wp-content/uploads/2015/10/povrsine_u_geometriji.pdf}{MNM predavanju o metodi površine.}
Kao rješenje upišite najmanji prosti broj djeljiv s $1$.
 simetrale šiljastih kutova
simetrale šiljastih kutova 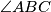 i
i 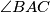 sijeku katete
sijeku katete  i
i  redom u točkama
redom u točkama  i
i  . Ako se pravci
. Ako se pravci  i
i 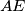 sijeku u točki
sijeku u točki  , dokažite
, dokažite 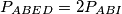

 simetrala kuta
simetrala kuta 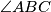 vrijedi
vrijedi 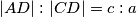 i
i 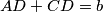 , nije teško vidjeti da
, nije teško vidjeti da 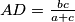 i
i 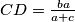 . Na isti način zaključujemo i da je
. Na isti način zaključujemo i da je 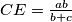 i
i 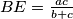 .
. Sada želimo izraziti površinu četverokuta
Sada želimo izraziti površinu četverokuta 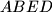 preko površine
preko površine 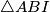 .
.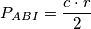 Kako je
Kako je 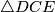 pravokutan, čini nam se zgodno izraziti
pravokutan, čini nam se zgodno izraziti 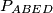 kao
kao 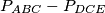 . Računamo:
. Računamo: 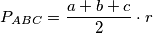
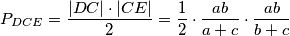 Čini nam se problematično što se u formuli za površinu
Čini nam se problematično što se u formuli za površinu  ne pojavljuje
ne pojavljuje  , ali kako je trokut
, ali kako je trokut  pravokutan, lako možemo izračunati koliki mora biti
pravokutan, lako možemo izračunati koliki mora biti  pa ga uključiti u formulu. Iz
pa ga uključiti u formulu. Iz 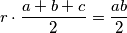 slijedi da je
slijedi da je 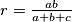 , stoga je
, stoga je 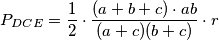
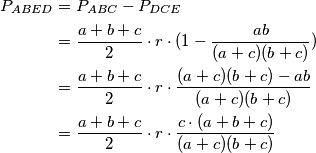
 :
: 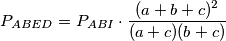
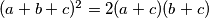 , gotovi smo. Raspisujemo:
, gotovi smo. Raspisujemo: 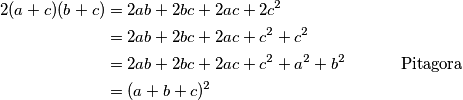
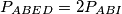 što je trebalo dokazati. Malo drugačije rješenje ovog zadatka i još puno sličnih primjera možete pronaći u MNM predavanju o metodi površine.
što je trebalo dokazati. Malo drugačije rješenje ovog zadatka i još puno sličnih primjera možete pronaći u MNM predavanju o metodi površine. .
. 