Primjer 1. Dana je kružnica  te točka
te točka  izvan nje. Kroz
izvan nje. Kroz  su povučena dva pravca koji sijeku danu kružnicu u
su povučena dva pravca koji sijeku danu kružnicu u  i
i  , odnosno
, odnosno  i
i  . Dokažite da vrijedi
. Dokažite da vrijedi 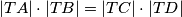 .
.
Rješenje.
Sa MNM predavanja 1.zadatak:
Neka su točke 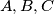 i
i  vrhovi četverokuta tim redom. Trokuti
vrhovi četverokuta tim redom. Trokuti 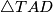 i
i 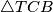 imaju zajednički kut pri
imaju zajednički kut pri  te su kutevi
te su kutevi 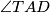 i
i 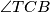 jednaki jer je četverokut tetivan. Naime,
jednaki jer je četverokut tetivan. Naime, 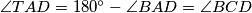 . Sada slijedi da su ta dva trokuta slična pa imamo
. Sada slijedi da su ta dva trokuta slična pa imamo 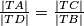 , iz čega dobivamo
, iz čega dobivamo 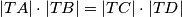 .
.
Napomena.
1) Neke oznake koje se koriste za potenciju točke  na kružnicu
na kružnicu  :
: 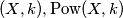 .
.
2) Ukoliko bi pomicali sekantu 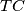 , tj. približavali točke
, tj. približavali točke  i
i  te naposlijetku dobili tangentu iz točke
te naposlijetku dobili tangentu iz točke  na kružnicu
na kružnicu  (
(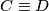 )
) 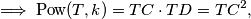 što drugačije možemo zapisati, koristeći Pitagorin poučak,
što drugačije možemo zapisati, koristeći Pitagorin poučak, 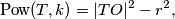 gdje je
gdje je  središte
središte  te
te  pripadni radijus, izraz može biti negativan ukoliko
pripadni radijus, izraz može biti negativan ukoliko  bude unutar kružnice.
bude unutar kružnice.
3) Sličan dokaz vrijedi i za  unutar kružnice, dok
unutar kružnice, dok 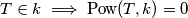 .
.
4) Naime, vrijedi i obrat, ukoliko vrijedi 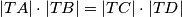 (i
(i  je na dužinama
je na dužinama  i
i  ili
ili  nije na nijednoj od njih) onda je četverokut
nije na nijednoj od njih) onda je četverokut  tetivan, tj. postoji kružnica na kojoj se te točke nalaze.
tetivan, tj. postoji kružnica na kojoj se te točke nalaze.
5) Broj koji upisujete kao rješenje je broj ove napomene.
\textbf{Primjer 1.} Dana je kružnica $k$ te točka $T$ izvan nje. Kroz $T$ su povučena dva pravca koji sijeku danu kružnicu u $A$ i $B$, odnosno $C$ i $D$. Dokažite da vrijedi $|T A| \cdot |T B| = |T C| \cdot |T D|$. \\ \\
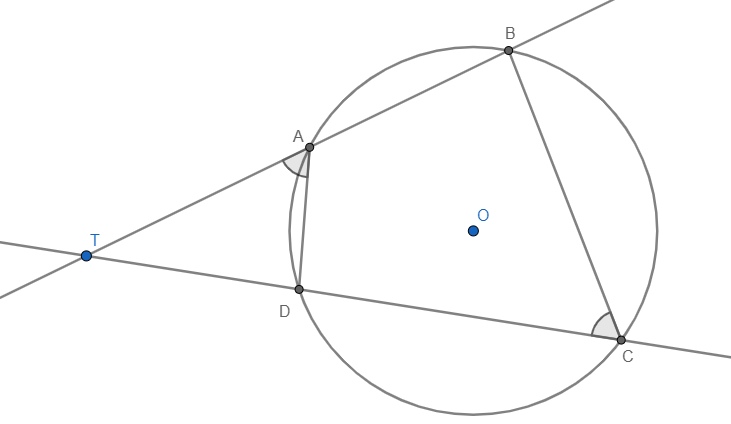
\textbf{Rješenje.} \\
\includegraphics{pop1.png}
\href{https://www.skoljka.org/media/attachment/1/00116_48xzf99ba0cr2eexgop8/potencija_tocke.pdf}{Sa MNM predavanja 1.zadatak:} \\
Neka su točke $A, B, C$ i $D$ vrhovi četverokuta tim redom. Trokuti $\triangle TAD$ i $\triangle TCB$ imaju zajednički kut pri $T$ te su kutevi $\angle TAD$ i $\angle TCB$ jednaki jer je četverokut tetivan. Naime, $\angle TAD = 180^{\circ} - \angle BAD=\angle BCD$. Sada slijedi da su ta dva trokuta slična pa imamo $\frac{|TA|}{|TD|} =\frac{|TC|}{|TB|}$, iz čega dobivamo
$|TA| \cdot |TB|= |TC| \cdot |TD|$. \\ \\
Napomena.
1) Neke oznake koje se koriste za potenciju točke $X$ na kružnicu $k$: $(X, k), \text{Pow}(X, k)$.
2) Ukoliko bi pomicali sekantu $TC$, tj. približavali točke $C$ i $D$ te naposlijetku dobili tangentu iz točke $T$ na kružnicu $k$ ($C \equiv D$)
$$\implies \text{Pow}(T, k) = TC\cdot TD = TC^2,$$
što drugačije možemo zapisati, koristeći Pitagorin poučak,
$$\text{Pow}(T, k) = |TO|^2-r^2,$$
gdje je $O$ središte $k$ te $r$ pripadni radijus, izraz može biti negativan ukoliko $T$ bude unutar kružnice.
3) Sličan dokaz vrijedi i za $T$ unutar kružnice, dok $T \in k \implies \text{Pow}(T, k) = 0$.
4) Naime, vrijedi i obrat, ukoliko vrijedi $|TA| \cdot |TB|= |TC| \cdot |TD|$ (i $T$ je na dužinama $AB$ i $CD$ ili $T$ nije na nijednoj od njih) onda je četverokut $ABCD$ tetivan, tj. postoji kružnica na kojoj se te točke nalaze.
5) Broj koji upisujete kao rješenje je broj ove napomene.
 te točka
te točka  izvan nje. Kroz
izvan nje. Kroz  su povučena dva pravca koji sijeku danu kružnicu u
su povučena dva pravca koji sijeku danu kružnicu u  i
i  , odnosno
, odnosno  i
i  . Dokažite da vrijedi
. Dokažite da vrijedi 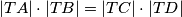 .
. 
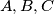 i
i  vrhovi četverokuta tim redom. Trokuti
vrhovi četverokuta tim redom. Trokuti 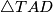 i
i 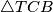 imaju zajednički kut pri
imaju zajednički kut pri  te su kutevi
te su kutevi 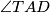 i
i 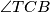 jednaki jer je četverokut tetivan. Naime,
jednaki jer je četverokut tetivan. Naime, 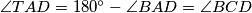 . Sada slijedi da su ta dva trokuta slična pa imamo
. Sada slijedi da su ta dva trokuta slična pa imamo 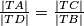 , iz čega dobivamo
, iz čega dobivamo 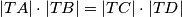 .
.  na kružnicu
na kružnicu  :
: 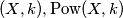 .
.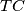 , tj. približavali točke
, tj. približavali točke  i
i  te naposlijetku dobili tangentu iz točke
te naposlijetku dobili tangentu iz točke  na kružnicu
na kružnicu  (
(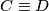 )
) 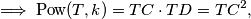 što drugačije možemo zapisati, koristeći Pitagorin poučak,
što drugačije možemo zapisati, koristeći Pitagorin poučak, 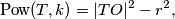 gdje je
gdje je  središte
središte  te
te  pripadni radijus, izraz može biti negativan ukoliko
pripadni radijus, izraz može biti negativan ukoliko  bude unutar kružnice.
bude unutar kružnice. unutar kružnice, dok
unutar kružnice, dok 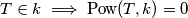 .
.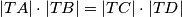 (i
(i  je na dužinama
je na dužinama  i
i  ili
ili  nije na nijednoj od njih) onda je četverokut
nije na nijednoj od njih) onda je četverokut  tetivan, tj. postoji kružnica na kojoj se te točke nalaze.
tetivan, tj. postoji kružnica na kojoj se te točke nalaze.