Vrijeme: 01:57
PT i TČ - Primjer 2
Primjer 2. Neka su  i
i  dvije kružnice koje se sijeku u točkama
dvije kružnice koje se sijeku u točkama  i
i  . Dokažite da je pravac
. Dokažite da je pravac  geometrijsko mjesto svih točaka koje imaju jednaku potenciju na obje kružnice.
geometrijsko mjesto svih točaka koje imaju jednaku potenciju na obje kružnice.
Rješenje.
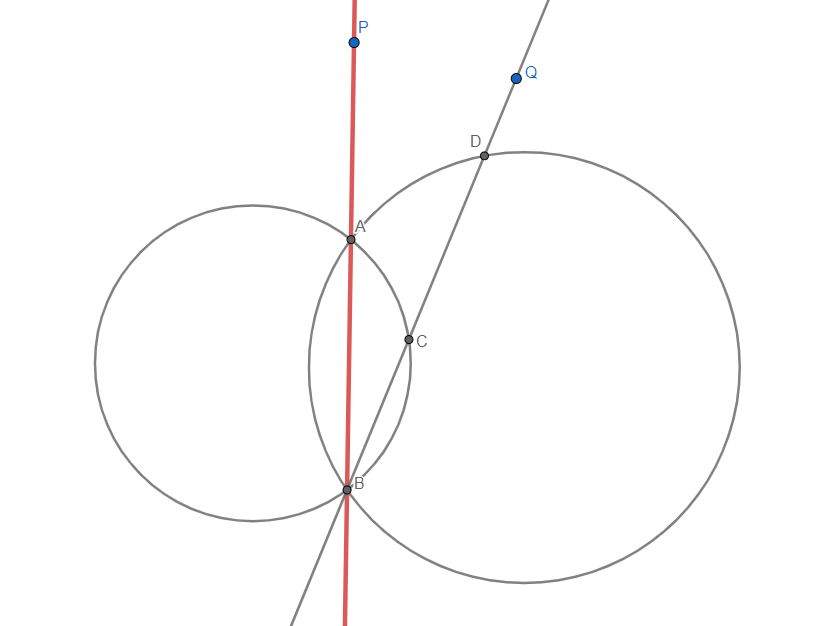
Neka je  proizvoljna točka na
proizvoljna točka na  , tada
, tada 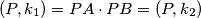 , čime smo dokazali da sve točke na pravcu imaju jednaku potenciju na obje kružnice.
, čime smo dokazali da sve točke na pravcu imaju jednaku potenciju na obje kružnice.
Pretpostavimo da postoji točka  koja se ne nalazi na
koja se ne nalazi na  takva da ima jednaku potenciju na obje kružćnice, tada pravac
takva da ima jednaku potenciju na obje kružćnice, tada pravac 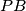 siječe
siječe  i
i  u
u  i
i  (različite od
(različite od  ,
, 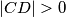 ), redom. No sada imamo
), redom. No sada imamo 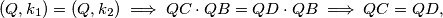 što daje kontradikciju (budući da se
što daje kontradikciju (budući da se  ne nalazi između
ne nalazi između  i
i  ) te time i tvrdnju zadatka.
) te time i tvrdnju zadatka.
Tada pravac  zovemo radikalna os kružnica
zovemo radikalna os kružnica  i
i  .
.
Upišite broj točaka sa skice.
