MetaMath '22

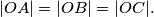
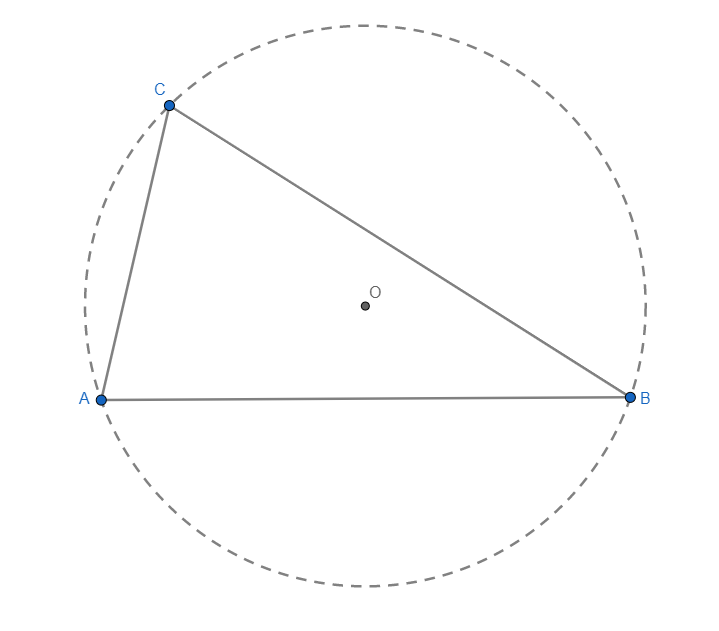
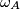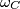\textbf{Primjer 3.} Dokaži da u trokutu $ABC$ postoji središte opisane kružnice. Odnosno, da postoji točka $O$ tako da je $$|OA| = |OB| = |OC|.$$ \\ \textbf{Rješenje.} \\ \includegraphics{pop3.png} Konstruirajte kružnicu polumjera nula (!) sa središtem u $A$ i označite je s $\omega_A$. Definiramo $\omega_B$ i $\omega_C$ slično. Budući da centri nisu kolinearni, možemo pronaći njihovo \textbf{radikalno središte} $O$ (Vidi \href{https://mnm.hr/wp-content/uploads/2016/03/potencija_tocke.pdf}{zadatak 10.} MNM predavanje). 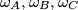Sada znamo da su potencije od $O$ do svakog od $\omega_A, \omega_B, \omega_C$ jednake. Preformulirano, (kvadrat) duljine "tangenti" na svaku kružnicu su jednake: to jest, 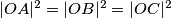$|OA|^2 = |OB|^2 = |OC|^2$. (Da vidite da je 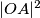$|OA|^2$ stvarno potencija točke, samo upotrijebite Pow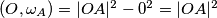$(O, \omega_A) = |OA|^2-0^2 = |OA|^2$.) Odavde izvodimo da je 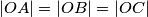$|OA| = |OB| = |OC|$, kako se i tražilo. \\ \\ Kolika je suma radijusa kružnica koje smo promatrali?