Dvostruko prebrojavanje: uvod
Lijep pozdrav svima! Dobrodošli na još jedan kombinatorni tjedan. Ovaj put bavit ćemo se metodom matematičke indukcije i metodom dvostrukog prebrojavanja. Ovdje ćemo pogledati nekoliko riješenih primjera glede dvostukog prebrojavanja. Ta metoda se najčešće koristi kada želimo dokazati neki identitet 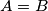 pri čemu na oba izraza
pri čemu na oba izraza  i
i  možemo gledati na kombinatorni način (u zadacima su to često sume i produkti binomnih koeficijenata ili pak faktorijela). Rješavanje takvih zadataka možemo svesti na tri djela:
možemo gledati na kombinatorni način (u zadacima su to često sume i produkti binomnih koeficijenata ili pak faktorijela). Rješavanje takvih zadataka možemo svesti na tri djela: 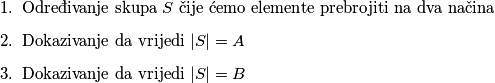 Tada princip dvostrukog prebrojavanja kaže da vrijedi
Tada princip dvostrukog prebrojavanja kaže da vrijedi 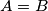 , pa smo time dokazali traženi identitet. No najprije ćemo ponoviti nekoliko definicija i kombinatorno dokazati dva korisna rezultata.
, pa smo time dokazali traženi identitet. No najprije ćemo ponoviti nekoliko definicija i kombinatorno dokazati dva korisna rezultata.
Najprije, faktorijel prirodnog broja  definira se kao produkt svih prirodnih brojeva manjih ili jednakih od broja
definira se kao produkt svih prirodnih brojeva manjih ili jednakih od broja  i obično se označava sa
i obično se označava sa 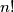 . Dakle,
. Dakle, 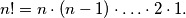 Obično još dogovorno stavljamo
Obično još dogovorno stavljamo 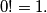
Neka su sada  i
i  cijeli brojevi takvi da je
cijeli brojevi takvi da je 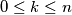 . Definiramo
. Definiramo 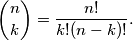 Broj
Broj 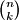 nazivamo binomni koeficijent (drugi rješeni primjer opravdava naziv tog broja).
nazivamo binomni koeficijent (drugi rješeni primjer opravdava naziv tog broja).
