Vrijeme: 15:45

Primjer 1

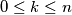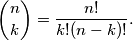
Neka je S skup sa n elemenata i neka je 0\leq k\leq n. Tada je broj podskupova s k-elemenata od S jednak \binom{n}{k}=\frac{n!}{k!(n-k)!}.

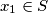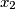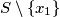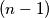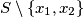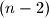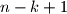Dokaz. Na koliko načina možemo izdvojiti k elemenata iz skupa S? Prvi element x_1\in S možemo od odabrati na n načina. Drugi element x_2 zapravo biramo iz skupa S\setminus\{x_1\} pa imamo (n-1) mogućnost. Treći element biramo iz skupa S\setminus\{x_1,x_2\} pa imamo (n-2) mogućnosti. Nastavljajući ovaj postupak vidimo da za k-ti element imamo n-k+1 mogućnost. Slijedi da ukupno imamo 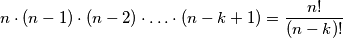n\cdot(n-1)\cdot(n-2)\cdot\ldots\cdot(n-k+1)=\frac{n!}{(n-k)!} mogućnosti. Greška koju smo napravili u gornjoj diskusiji je ta što smo napravili neki poredak unutar tog podskupa, a ne bismo smjeli razlikovati elemente (koji je prvi, koji je drugi, ...). Stoga smo neke iste podskupove brojali više puta. Gornji broj moramo podijeliti s brojem različitih redoslijeda k elemenata unutar podskupa kojeg biramo. Imamo k mogućnosti za odabrati prvi element, k-1 za drugi... 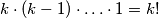ukupno imamo k\cdot(k-1)\cdot\ldots\cdot 1=k! mogućnosti, pa slijedi da je traženi broj podskupova jednak 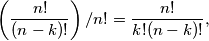\left(\frac{n!}{(n-k)!}\right)/n!=\frac{n!}{k!(n-k)!}, što smo i trebali vidjeti.

Kao rješenje upišite 0.