MetaMath '22

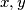\textbf{Binomni teorem}. Neka je $n$ prirodan broj i neka su $x,y$ realni brojevi. Dokažite da vrijedi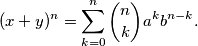 $$(x+y)^n=\sum_{k=0}^{n}\binom{n}{k}a^kb^{n-k}.$$ \textbf{Dokaz}. Promotrimo izraz s lijeve strane: 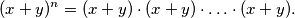$$(x+y)^n=(x+y)\cdot(x+y)\cdot\ldots\cdot(x+y).$$ Jedan način da se ovaj izraz raspiše je sljedeći: iz svake zagrade uzmemo jednu od varijabli $x$ ili $y$ i izmnožimo sve izabrane članove. Zatim sumiramo sve te produkte za sve različite odabire varijabli. 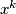Izraz $x^k$ dobivamo kada iz $k$ zagrada biramo element $x$ (a onda iz preostalih zagrada moramo birati $y$). Dakle, trebamo odabrati $k$ zagrada od njih $n$ iz kojih ćemo uzeti varijablu $x$. 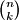To možemo napraviti na $\binom{n}{k}$ načina. 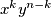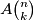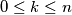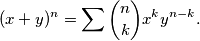Dakle, koeficijent uz $x^ky^{n-k}$ je $A\binom{n}{k}$, pa kad sumiramo po svim $0\leq k\leq n$ (možemo birati od $0$ $x$-eva pa sve do $n$ $x$-eva) dobivamo $$(x+y)^n=\sum\binom{n}{k}x^ky^{n-k}.$$ Kao rješenje upišite $0$.