Vrijeme: 15:21

Primjer 3.

U sljedećem primjeru ilustrirat ćemo tipičnu primjernu principa dvostrukog prebrojavanja pri dokazivanju kombinatornog identiteta.

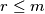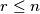Primjer. Neka su n i m i prirodni brojevi i neka je r prirodan broj takav da r\leq m i r\leq n. Dokažite da vrijedi: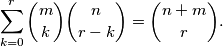 \sum_{k=0}^{r}\binom{m}{k}\binom{n}{r-k}=\binom{n+m}{r}.

Rješenje U rješenju zadatka poslužit ćemo se malo slobodnijim rječnikom kako bi lakše zamislili situaciju.

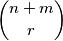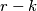U razredu s n dječaka i m djevojčica trebamo odabrati njih r koji će nastupiti u školskom natjecanju graničara. Taj odabir možemo napraviti na \binom{n+m}{r} načina. S druge strane, taj odabir možemo napraviti i ovako: najprije od m djevojaka biramo njih k koje će se natjecati, a zatim od n dječaka biramo njih r-k koji će se natjecati. Djevojke možemo odabrati na 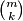\binom{m}{k} načina, a dečke na 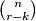\binom{n}{r-k} načina. 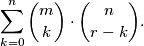Budući da djevojčica možemo odabrati sve od 0 do r slijedi da je ukupan broj mogućnosti jednak \sum_{k=0}^n\binom{m}{k}\cdot\binom{n}{r-k}. Po principu dvostrukog prebrojavanja zaključujemo da je 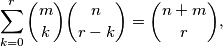\sum_{k=0}^{r}\binom{m}{k}\binom{n}{r-k}=\binom{n+m}{r}, što smo i trebali vidjeti.

Kao rješenje upišite 0.