Primjer 4.
Dokažite da vrijedi 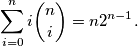
Rješenje Razred od  učenika potrebno je odabrati njih
učenika potrebno je odabrati njih  koji bi išli na šahovsko natjecanje (moguće je da nitko nije odabran) i od tih
koji bi išli na šahovsko natjecanje (moguće je da nitko nije odabran) i od tih  učenika treba odabrati kapetana momčadi koji će igrati na prvoj ploči. Od
učenika treba odabrati kapetana momčadi koji će igrati na prvoj ploči. Od  učenika biramo njih
učenika biramo njih  , za što imamo
, za što imamo  mogućnosti. Zatim od tih
mogućnosti. Zatim od tih  biramo jednog koji će biti kapetan, za što imamo
biramo jednog koji će biti kapetan, za što imamo  mogućnosti. Kako možemo odabrati od
mogućnosti. Kako možemo odabrati od  do učenika od
do učenika od  učenika slijedi da je ukupan broj mogućnosti
učenika slijedi da je ukupan broj mogućnosti 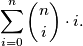
Odabir možemo napraviti i na sljedeći način: najprije biramo kapetana ekipe, što možemo napraviti na  načina. Zatim od preostalog broja učenika (
načina. Zatim od preostalog broja učenika ( ) za svakog imamo mogućnost da ide ili ne, što je
) za svakog imamo mogućnost da ide ili ne, što je 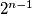 mogućnosti. Stoga je ukupan broj mogućnosti
mogućnosti. Stoga je ukupan broj mogućnosti 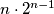 .
.
Po principu dvostrukog prebrojavanja zaključujemo da ta dva broja trebaju biti jednaka, odnosno 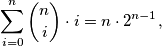 što smo i trebali vidjeti.
što smo i trebali vidjeti.
Kao rješenje upišite  .
.
