MetaMath '22

Na zabavi od $17$ ljudi svaka osoba tvrdi da se je rukovala sa točno petero ljudi. Dokažite da barem jedna osoba ne govori istinu. \textbf{Rješenje}. Tvrdnju ćemo dokazati pomoću principa kontradikcije. Pretpostavimo da svi ljudi govore istinu. Fiksirajmo neki poredak ljudi i označimo ih brojevima 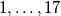$1,\ldots,17$. Pretpostavimo da je ukupno bilo $n$ rukovanja. Označimo ta rukovanja sa $r_1,r_2,\ldots,r_n$. 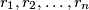Promotrimo sljedeći skup 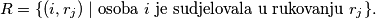$$R=\{(i,r_j)\;|\;\text{osoba $i$ je sudjelovala u rukovanju $r_j$}\}.$$ Prebrojat ćemo elemente skupa $R$ na dva načina (najprije po prvoj, a zatim po drugoj varijabli). 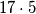Prvo, budući da svi ljudi po pretpostavci govore istinu, svatko od $17$ ljudi sudjelovao je u točno $5$ rukovanja pa skup $R$ ima $17\cdot 5$ elemenata. Fokusirajmo se sada na rukovanja. U svakom rukovanju sudjelovalo je točno dvoje ljudi. 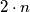Budući da je bilo $n$ rukovanja slijedi da skup $S$ ima $2\cdot n$ elemenata. Po principu dvostrukog prebrojavanja zaključujemo da su dobiveni brojevi jednaki, odnosno vrijedi 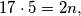$$17\cdot 5=2n,$$ što nije moguće. Naime, broj rukovanja $n$ je prirodan broj. Lijeva strana jednakosti je neparan, a desna strana je paran broj. Zaključujemo da nam je pretpostavka bila kriva; Barem jedna osoba ne govori istinu. Kao rješenje upišite $0$.