Primjer 7.
Neka su 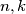 prirodni brojevi i neka je
prirodni brojevi i neka je  skup od
skup od  točaka takvih da za svaku točku
točaka takvih da za svaku točku  iz skupa
iz skupa  postoji barem
postoji barem  točaka iz skupa
točaka iz skupa  koje su jednako udaljene od točke
koje su jednako udaljene od točke  . Dokažite da vrijedi
. Dokažite da vrijedi 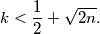
Dokaz. Najprije ćemo danu nejednakost prevesti u ekvivalentnu koja će nam biti korisnija. Imamo 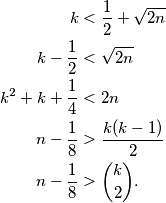 Budući da su
Budući da su  i
i 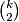 prirodni brojevi, gornja nejednakost vrijedi ako i samo ako vrijedi nejednakost:
prirodni brojevi, gornja nejednakost vrijedi ako i samo ako vrijedi nejednakost: 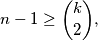 koju ćemo i dokazati. Spojimo svaku točku skupa
koju ćemo i dokazati. Spojimo svaku točku skupa  sa svakom drugom točkom. Prebrojat ćemo tako nastale bridove na dva načina.
sa svakom drugom točkom. Prebrojat ćemo tako nastale bridove na dva načina.
Kako skup  ima
ima  različitih točaka ukupno ima
različitih točaka ukupno ima 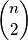 brida (odaberemo dvije točke i spojimo ih bridom).
brida (odaberemo dvije točke i spojimo ih bridom).
S druge strane, po pretpostavci svaka točka skupa  ima barem
ima barem  točaka jednako udaljenih od nje. Uzmimo proizvoljnu točku
točaka jednako udaljenih od nje. Uzmimo proizvoljnu točku  skupa
skupa  i nacrtajmo kružnicu sa središtem u
i nacrtajmo kružnicu sa središtem u  i polumjerom takvim da siječe skup
i polumjerom takvim da siječe skup  u barem
u barem  točaka
točaka 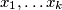 . Tada je svaka dužina
. Tada je svaka dužina 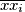 ujedno i polumjer te kružnice i brid koji želimo prebrojati. Ponovimo li ovaj postupak za svaku točku dobivamo da tako konstruiranih bridova, brojeći kratnost (nismo orijentirali dužinu), ima barem
ujedno i polumjer te kružnice i brid koji želimo prebrojati. Ponovimo li ovaj postupak za svaku točku dobivamo da tako konstruiranih bridova, brojeći kratnost (nismo orijentirali dužinu), ima barem 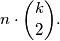 Uzmimo proizvoljne dvije točke skupa
Uzmimo proizvoljne dvije točke skupa  i pripadne konstruirane kružnice. Neka je
i pripadne konstruirane kružnice. Neka je  središte prve kružnice i neka je
središte prve kružnice i neka je 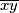 neki njen polumjer. Ako druga kružnica ima isti polumjer
neki njen polumjer. Ako druga kružnica ima isti polumjer 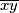 tada je središte druge kružnice ili
tada je središte druge kružnice ili  ili
ili  . Ukoliko bi to bio
. Ukoliko bi to bio  tada bi se kružnice poklapale pa bi bile iste. Dakle, središte je
tada bi se kružnice poklapale pa bi bile iste. Dakle, središte je  a polumjer
a polumjer 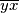 . Ovo pokazuje da dvije različite kružnice dijele najviše jedan polumjer. Stoga smo najviše
. Ovo pokazuje da dvije različite kružnice dijele najviše jedan polumjer. Stoga smo najviše 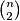 brojali dvaput, pa različitih bridova dobivenih ovom konstrukcijom ima barem
brojali dvaput, pa različitih bridova dobivenih ovom konstrukcijom ima barem 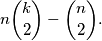 Taj broj nije veći od ukupnog broja bridova, što daje nejednakost
Taj broj nije veći od ukupnog broja bridova, što daje nejednakost 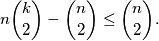 Iz ovoga lako slijedi nejednakost koju trebamo pokazati
Iz ovoga lako slijedi nejednakost koju trebamo pokazati 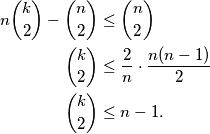
Kao rješenje upišite  .
.
