MetaMath '22

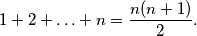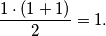Dokažite da za svaki prirodan broj $n$ vrijedi jednakost: $$ 1+2+\ldots+n=\frac{n(n+1)}{2} . $$ Dokaz provodimo matematičkom indukcijom po broju $n$. BAZA INDUKCIJE Trebamo dokazati da navedena jednakost vrijedi za broj $n=1$. Lijeva strana jednakosti zapravo predstavlja zbroj svih brojeva od 1 do $n$ pa je u ovom slučaju jednaka 1, dok je desna strana jednaka $$ \frac{1 \cdot(1+1)}{2}=1 . $$ Dakle, imamo jednakost 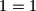$1=1$ koja očito vrijedi, pa je baza dokazana. PRETPOSTAVKA INDUKCIJE Pretpostavimo da jednakost 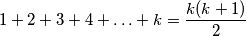$$ 1+2+3+4+\ldots+k=\frac{k(k+1)}{2} $$ vrijedi za neki $k \in \mathbb{N}$. KORAK INDUKCIJE Trebamo dokazati da jednakost vrijedi i za $k+1$, odnosno da vrijedi $$ 1+2+3+4+\ldots+(k+1)=\frac{(k+1)(k+2)}{2} . 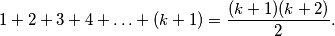$$ Lijevu stranu možemo raspisati koristeći pretpostavku: 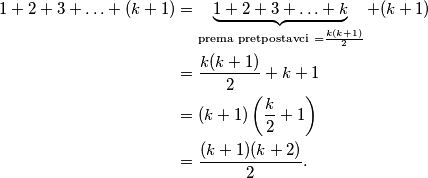$$ \begin{aligned} 1+2+3+\ldots+(k+1) &=\underbrace{1+2+3+\ldots+k}_{\text {prema pretpostavci }=\frac{k(k+1)}{2}}+(k+1) \\ &=\frac{k(k+1)}{2}+k+1 \\ &=(k+1)\left(\frac{k}{2}+1\right) \\ &=\frac{(k+1)(k+2)}{2} . \end{aligned} $$ Ovime je korak indukcije dokazan, pa tvrdnja zadatka vrijedi za svaki $n \in \mathbb{N}$. Upišite 1 za idući primjer.