Vrijeme: 20:24

Indukcija - Uvod 3

Dokaze matematičkom indukcijom možemo koristiti i kod dokazivanja tvrdnji koje vrijede za sve prirodne brojeve koji su veći ili jednaki 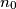n_0, gdje je 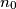n_0 neki prirodni broj. Tada se princip matematičke indukcije može izreći ovako:

Generalizirani princip matematičke indukcije \begin{itemize} \item[(i)] Baza indukcije: Tvrdnja koju trebamo dokazati vrijedi za $n=n_0$. \item[(ii)] Pretpostavka indukcije: Pretpostavljamo da tvrdnja koju trebamo dokazati vrijedi za neki $k \in \mathbb{N}$. \item[(iii)] Korak indukcije. \end{itemize}

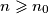Ako iz pretpostavke indukcije slijedi da tvrdnja koju trebamo dokazati vrijedi i za broj k+1, onda navedena tvrdnja vrijedi za svaki prirodan broj n \geqslant n_0. Uočite da je princip koji smo prije koristili zapravo gornji princip za 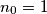n_0=1. Upamtite, baza indukcije je uvijek najmanji broj 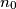n_0 od svih brojeva na koje se tvrdnja odnosi. Pogledajmo sljedeći primjer. Dokažimo nejednakost: 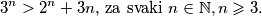3^n>2^n+3 n \text {, za svaki } n \in \mathbb{N}, n \geqslant 3 . Tvrdnju ćemo dokazati korištenjem prethodno spomenutog principa matematičke indukcije za n_0=3.

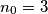BAZA INDUKCIJE Za 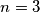n=3 imamo nejednakost 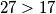27>17 koja očito vrijedi.

PRETPOSTAVKA INDUCKIJE Pretpostavimo da postoji 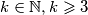k \in \mathbb{N}, k \geqslant 3 takav da vrijedi nejednakost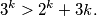 3^k>2^k+3 k .

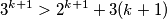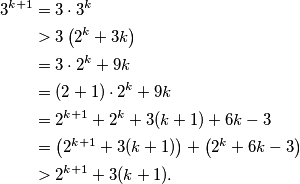KORAK INDUCKIJE Dokazujemo tvrdnju za k+1, tj da je 3^{k+1}>2^{k+1}+3(k+1) Vrijedi \begin{aligned} 3^{k+1} &=3 \cdot 3^k \\ &>3\left(2^k+3 k\right) \\ &=3 \cdot 2^k+9 k \\ &=(2+1) \cdot 2^k+9 k \\ &=2^{k+1}+2^k+3(k+1)+6 k-3 \\ &=\left(2^{k+1}+3(k+1)\right)+\left(2^k+6 k-3\right) \\ &>2^{k+1}+3(k+1) . \end{aligned} Posljednja nejednakost vrijedi zbog 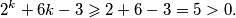2^k+6 k-3 \geqslant 2+6-3=5>0 . Upišite 1 za novi primjer.