MetaMath '22

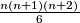Ping-pong loptice možemo složiti u pravilnu trostranu piramidu tako da donji sloj složimo u jednakostranični trokut s $n$ loptica duž stranice, idući sloj u trokut s $n-1$ loptica duž stranice, itd. Dokažimo da je za piramidu od $n$ slojeva potrebno $\frac{n(n+1)(n+2)}{6}$ loptica. BAZA INDUKCIJE Za $n=1$ tvrdnja očito vrijedi jer se piramida od jednog sloja sastoji od samo jedne loptice te imamo jednakost $1=\frac{1 \cdot(1+1) \cdot(1+2)}{6}$. 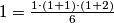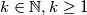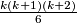PRETPOSTAVKA INDUKCIJE Pretpostavimo da tvrdnja vrijedi za neki $k \in \mathbb{N}, k \geq1$, odnosno da je za piramidu od $k$ slojeva potrebno $\frac{k(k+1)(k+2)}{6}$ loptica. KORAK INDUKCIJE Dokazujemo tvrdnju za piramidu od $k+1$ slojeva. Uočimo da takvu piramidu dobivamo kada piramidi od $k$ slojeva dodamo još jedan, najdonji sloj. Dakle, potreban broj loptica jednak je zbroju broja loptica u tom najdonjem sloju i broja loptica potrebnih za izgradnju piramide od $k$ slojeva. Prema pretpostavci, drugi broj jednak je $\frac{k(k+1)(k+2)}{6}$. 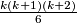Znači sada još samo trebamo izračunati broj loptica u jednakostraničnom trokutu s $k+1$ loptica duž stranice. 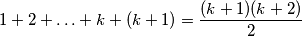Lako možemo zaključiti da se taj trokut sastoji od $$ 1+2+\ldots+k+(k+1)=\frac{(k+1)(k+2)}{2} $$ loptica, pri čemu posljednja jednakost slijedi iz prvog primjera. 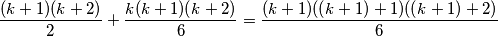Dakle, za izgradnju piramide od $k+1$ loptica potrebno je $$ \frac{(k+1)(k+2)}{2}+\frac{k(k+1)(k+2)}{6}=\frac{(k+1)((k+1)+1)((k+1)+2)}{6} $$ loptica. Korak indukcije je dokazan, pa vrijedi tvrdnja zadatka.