Vrijeme: 01:52
Indukcija - Uvod 5
Pokažimo da 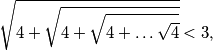 pri čemu korijena ima
pri čemu korijena ima  .
.
Za  označimo
označimo 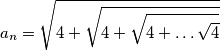 pri čemu u gornjem izrazu ima
pri čemu u gornjem izrazu ima  korijena. Tvrdimo da je
korijena. Tvrdimo da je 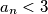 , za svaki
, za svaki  .
.
BAZA INDUKCIJE Za  imamo
imamo 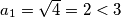 .
.
PRETPOSTAVKA INDUKCIJE Pretpostavimo da 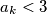 , za neki
, za neki  .
.
KORAK INDUKCIJE Dokazujemo tvrdnju zadatka za  . Uočimo da je
. Uočimo da je 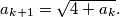 Sada je prema pretpostavci
Sada je prema pretpostavci 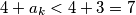 , a onda je
, a onda je 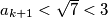 . Tražena nejednakost dakle vrijedi i za
. Tražena nejednakost dakle vrijedi i za  .
.
Upišite 1 za kraj uvodog lanca.
