Indukcija - Teži 1
Susreli smo se već s klasičnom matematičkom indukcijom - ako pokažemo dvije stvari: neka tvrdnja vrijedi za  (baza indukcije) i ukoliko tvrdnja vrijedi za
(baza indukcije) i ukoliko tvrdnja vrijedi za  (pretpostavka indukcije), tada vrijedi i za
(pretpostavka indukcije), tada vrijedi i za  (korak indukcije), pokazali smo da tvrdnja vrijedi za svaki prirodan broj
(korak indukcije), pokazali smo da tvrdnja vrijedi za svaki prirodan broj  . Klasična matematička indukcija ima svoje varijacije, a s nekima od njih susrest ćemo se na ovom predavanju:
. Klasična matematička indukcija ima svoje varijacije, a s nekima od njih susrest ćemo se na ovom predavanju:
1. Što ako želimo pokazati da nešto vrijedi za parne brojeve? U bazi indukcije dokazat ćemo da tvrdnja vrijedi za  , a u koraku ćemo pokazati da ako tvrdnja vrijedi za
, a u koraku ćemo pokazati da ako tvrdnja vrijedi za  , tada vrijedi i za
, tada vrijedi i za 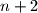 .
.
2. Za dokaz da tvrdnja vrijedi za  ponekad je potrebna pretpostavka da tvrdnja vrijedi za brojeve
ponekad je potrebna pretpostavka da tvrdnja vrijedi za brojeve 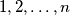 , a ne samo
, a ne samo  . U tom slučaju koristimo tzv. jaku indukciju i u praksi nema razlike, jaka indukcija od klasične razlikuje se samo u pretpostavci.
. U tom slučaju koristimo tzv. jaku indukciju i u praksi nema razlike, jaka indukcija od klasične razlikuje se samo u pretpostavci.
3. Što ako primjerice znam pokazati da ako tvrdnja vrijedi za  , tada vrijedi i za
, tada vrijedi i za  , te da tvrdnja vrijedi za neki beskonačni niz prirodnih brojeva, recimo niz potencija broja 2? Tada "regresivna" indukcija govori da tvrdnja vrijedi za sve prirodne brojeve.
, te da tvrdnja vrijedi za neki beskonačni niz prirodnih brojeva, recimo niz potencija broja 2? Tada "regresivna" indukcija govori da tvrdnja vrijedi za sve prirodne brojeve.
Upišite 1 za nastavak.
